题目内容
如图所示，在光滑的水平面上有一质量为M、倾角为θ的光滑斜面体，它的斜面上
有一质量为m的物块沿斜面下滑。关于物块下滑过
程的分析，下列说法中正确的是
有一质量为m的物块沿斜面下滑。关于物块下滑过
程的分析，下列说法中正确的是
| A．物块下滑过程中斜面对物块的支持力不做功 |
| B．物块下滑过程中斜面体和物块构成的系统动量守恒 |
| C．物块下滑过程中物块的机械能守恒 |
| D．斜面体对地面的压力小于（m+M）g |
D
物体下滑过程中，斜面对物体的支持力对物体做负功，所以物体的机械能减小；由于水平方向系统不受外力，所以系统水平方向动量守恒；
以物块和斜面组成的整体为研究对象，分析受力情况，作出力图，将物块的加速度分解为沿
水平和竖直两个方向，根据牛顿第二定律得：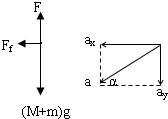
水平方向有：Ff=max=macosα
竖直方向有：（M+m）g-F=may=masinα
由于ax沿水平向左方向，则知摩擦力Ff向左．
由上得到：F=（M+m）g-masinα＞0，则F＜（M+m）g
本题对加速度不同的两个运用牛顿第二定律，运用正交分解法列方程：水平方向合力为：Fx=MaMx+mamx；竖直方向合力为：Fy=MaMy+mamy；要尝试使用，比较简单方便．
以物块和斜面组成的整体为研究对象，分析受力情况，作出力图，将物块的加速度分解为沿
水平和竖直两个方向，根据牛顿第二定律得：
水平方向有：Ff=max=macosα
竖直方向有：（M+m）g-F=may=masinα
由于ax沿水平向左方向，则知摩擦力Ff向左．
由上得到：F=（M+m）g-masinα＞0，则F＜（M+m）g
本题对加速度不同的两个运用牛顿第二定律，运用正交分解法列方程：水平方向合力为：Fx=MaMx+mamx；竖直方向合力为：Fy=MaMy+mamy；要尝试使用，比较简单方便．
练习册系列答案
能力评价系列答案
唐印文化课时测评系列答案
相关题目
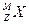连续经过三次α衰变和两次β衰变．若最后变成另一种元素的原子核Y，则新核Y的正确写法是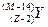
、
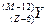
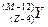
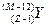
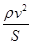
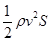
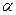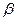和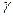
三种射线，由铅盒的小孔射出，在小孔外放一张铝箔，铝箔后的空间有一匀强电场。射线进入电场后，变为a、b两束，射线a沿原来方向行进，射线b发生了偏转，如图所示，则图中的射线a为_________射线，射线b为___________射线。
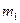的光滑弧形槽静止在光滑水平面上，底部与水平面平滑连接。一个质量为
的小球从槽
高处由静止开始下滑，要使小球能与弧形槽发生第二次作用，
