题目内容

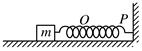
光滑曲面与竖直平面的交线是抛物线，如图所示，抛物线的方程是y=x2，下半部处在一个水平方向的匀强磁场中，磁场的上边界是y=a的直线（图中虚线所示），一个小金属环从抛物线上y=b（y>a）处以速度v沿抛物线下滑，假设抛物线足够长，金属环沿抛物线下滑后产生的焦耳热总量是（    ）
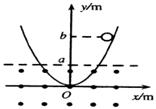
A．mgbB．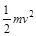
C．mg(b－a)D．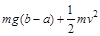
D

试题分析：最终金属块在磁场区与虚线a的交点之间来回摆动，交点设为O点，从最高点到O点由动能定理可知，D对
点评：本题要从能量守恒的角度考虑问题，只有当线圈进入和穿出磁场时才有感应电流产生，重力做功转化为了一部分的焦耳热
练习册系列答案
相关题目
如图所示，一轻弹簧左端与物体A相连，右端与物体B相连，开始时，A、B均在粗糙水平面上不动，弹簧处于原长状态。在物体B上作用一水平向右的恒力F，使物体A、B向右运动。在此过程中，下列说法中正确的为 （   ）

A．合外力对物体A所做的功等于物体A的动能增量
B．外力F做的功与摩擦力对物体B做的功之和等于物体B的动能增量
C．外力F做的功及摩擦力对物体A和B做功的代数和等于物体A和B的动能增量及弹簧弹性势能增量之和
D．外力F做的功加上摩擦力对物体B做的功等于物体B的动能增量与弹簧弹性势能增量之和
有一个边长为L=1.6m的正方形桌子,桌面离地高度为h=1.25m.一个质量为的小物块可从桌面正中心点以初速v0=3m/s沿着与OA成370的方向在桌面上运动直至落地.设动摩擦因数为μ="0.25" ,取g=10m/s2,求:

(1)物块落地的速度大小是多少?
(2)物块落地点到桌面中心点的水平距离是多少?
如图中（a）所示，一倾角为37o的传送带以恒定速度运行．现将一质量m=2kg的小物体以某一初速度放上传送带，物体相对地面的速度随时间变化的关系如图（b）所示．（取沿传送带向上为正方向，g=10m/s2，sin37o=0.6，cos37o=0.8）求：

（1）0~10s内物体位移的大小；
（2）物体与传送带间的动摩擦因数；
（3）0~10s内物体机械能增量及与传送带摩擦产生的热量Q．
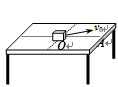
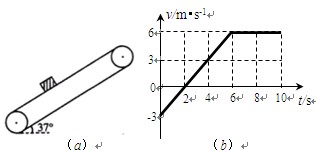
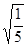如图所示，水平面上的轻弹簧一端与物体相连，另一端固定在墙上的P点，已知物体的质量为m=2．0 kg，物体与水平面间的动摩擦因数μ=0．4，弹簧的劲度系数k="200" N/m．现用力F拉物体，使弹簧从处于自然状态的O点由静止开始向左移动10 cm，这时弹簧具有弹性势能Ep=1．0 J，物体处于静止状态．取g="10" m/s2，撤去外力F后物体会向右滑动，第一次回到O点时的速度为m/s,则下列说法正确的是
A．物体向右滑动的距离可以达到12．5 cm
B．物体向右滑动的距离一定小于12．5 cm
C．物体向右滑动过程中速度等于m/s的位置有两个
D．物体到达最右端时动能为零，系统机械能也为零
（14分）如图所示，水平桌面上有一轻弹簧，左端固定在A点，自然状态时其右端位于B点。水平桌面右侧有一竖直放置的光滑轨道MNP，其形状为半径R=0.5m的圆环，MN为其竖直直径，P点到桌面的竖直距离h=2.4m。用质量m1=1.0kg的物块将弹簧缓慢压缩到C点，物块与水平桌面间的动摩擦因数μ=0.4，CB=0.5m，BD=2.5m，释放后弹簧恢复原长时物块恰停止在B点。现用同种材料、质量为m2=0.1kg的物块仍将弹簧缓慢压缩到C点释放，物块从桌面右端D飞离后，由P点沿切线落入圆轨道(g=10m/s2)。求：
（1）物块m2飞离桌面的速度大小
（2）物块m2在圆轨道P点时对轨道的压力大小
（3）物块m2的落地点与M点间的距离
质量为m的子弹以速度v水平射入放在光滑水平面上质量为M的木块中而不穿出，则(    )
A．子弹克服阻力做的功等于系统内能的增加
B．子弹动能的减少量与子弹克服阻力做功量相等
C．子弹损失的机械能等于木块获得的动能与系统损失的动能之和
D．阻力对子弹做的功等于子弹对木块所做的功
如图所示,在光滑水平面上有两个并排放置的木块A和B,已知mA="500" g,mB="300" g,有一质量为80 g的小铜球C以25  m/s的水平初速开始,在A表面滑动,由于C和A,B间有摩擦,铜块C最后停在B上,B和C一起以2.5  m/s的速度共同前进,求:

(1)木块A的最后速度vA′;
(2)C在离开A时速度vC′.
如图所示，两个质量相同的物体A和B，在同一高度处，A物体自由落下，B物体沿光滑斜面下滑，则它们到达地面时(空气阻力不计)

A．动能相同，速度相同。
B．A、B两物体在运动过程中机械能都守恒。
C．B物体的速率大，动能也大。
D．B物体重力所做的功比A物体重力所做的功多。

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网