Question

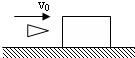
如图所示，质量为6kg的小球A与质量为3kg的小球B，用轻弹簧相连后在光滑的水平面上以速度v₀向左匀速运动，在A球与左侧墙壁碰，撞后两球继续运动的过程中，弹簧的最大弹性势能为4J，若A球与左墙壁碰撞前后无机械能损失，试求v₀的大小．

Answer 1

由于A球与左墙壁前后无机械能损失，所以A球与左侧墙壁碰撞后的速度大小仍为v₀，方向水平向右，如图甲所示．（1）
由题意分析可知，在A球与左侧墙壁后两球继续运动的过程中，当A、B小球的速度相等时（设大小为v，如图乙所示），弹簧的弹性势能最大．（2）
对于A、B小球和弹簧组成的系统，从甲图到乙图过程中，
由动量守恒定律得：m_Av₀-m_Bv₀=（m_A+m_B）v（3）
由机械能守恒得：

1

2

(mA+mB)

v

20

=

1

2

(mA+mB)v2+EP（4）
由（3）、（4）解得：v0=

(mA+mB)EP 2mAmB

=1m/s（5）
答：v₀的大小为1m/s．