题目内容
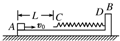
如图所示,一质量m1=0.45kg的平顶小车静止在光滑的水平轨道上.车顶右端放一质量m2=0.4kg的小物体,小物体可视为质点.现有一质量m0=0.05kg的子弹以水平速度v0=100m/s射中小车左端,并留在车中,已知子弹与车相互作用时间极短,小物体与车间的动摩擦因数为μ=0.5,最终小物体以5m/s的速度离开小车.g取10m/s2.求:
(1)子弹相对小车静止时,小车的速度大小;
(2)小车的长度.

(1)子弹相对小车静止时,小车的速度大小;
(2)小车的长度.

(1)子弹进入小车的过程中,子弹与小车组成的系统动量守恒,以子弹的初速度方向为正方向,由动量守恒定律得:
m0v0=(m0+m1)v1,
解得:v1=10m/s;
(2)子弹、物块、小车组成的系统动量守恒,以小车的速度方向为正方向,由动量守恒定律得:
(m0+m1)v1=(m0+m1)v2+m2v,
设小车长为L,对系统,由能量守恒定律得:
μm2gL=
(m0+m1)
-
(m0+m1)
-
m2v2,
解得:L=5.5m;
答:(1)子弹相对小车静止时,小车的速度大小为10m/s;
(2)小车的长度为5.5m.
m0v0=(m0+m1)v1,
解得:v1=10m/s;
(2)子弹、物块、小车组成的系统动量守恒,以小车的速度方向为正方向,由动量守恒定律得:
(m0+m1)v1=(m0+m1)v2+m2v,
设小车长为L,对系统,由能量守恒定律得:
μm2gL=
| 1 |
| 2 |
| v | 21 |
| 1 |
| 2 |
| v | 22 |
| 1 |
| 2 |
解得:L=5.5m;
答:(1)子弹相对小车静止时,小车的速度大小为10m/s;
(2)小车的长度为5.5m.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目



 ”形的光滑长直导轨槽,槽我向上(图为俯视图,图中两组平行双直线表示“
”形的光滑长直导轨槽,槽我向上(图为俯视图,图中两组平行双直线表示“ ”形槽的两侧壁).槽内放置六个滑块,滑块的手半部是半径为R的半圆柱形光滑凹槽,滑块的宽度为2R,恰与“
”形槽的两侧壁).槽内放置六个滑块,滑块的手半部是半径为R的半圆柱形光滑凹槽,滑块的宽度为2R,恰与“ ”形槽的两内侧壁的间距相等,滑块可在槽内沿槽壁自由滑动.现有六金属小球(可视为质点)以水平初速度Vj沿槽的六侧壁冲向滑块,从滑块的半圆形槽我边缘进入滑块凹槽.已知金属小球的质量为m,滑块的质量为3m,整个运动过程中无机械能损失.求:
”形槽的两内侧壁的间距相等,滑块可在槽内沿槽壁自由滑动.现有六金属小球(可视为质点)以水平初速度Vj沿槽的六侧壁冲向滑块,从滑块的半圆形槽我边缘进入滑块凹槽.已知金属小球的质量为m,滑块的质量为3m,整个运动过程中无机械能损失.求:

