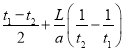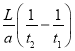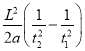Question

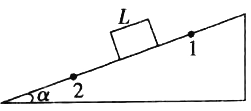
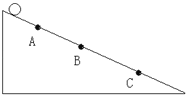
【题目】如图所示，LMN是竖直平面内固定的光滑绝缘轨道，MN水平且足够长，LM下端与MN相切。质量为m的带正电小球B静止在水平轨道上，质量为2m的带正电小球A从LM上距水平轨道高为h处由静止释放，在A球进入水平轨道之前，由于A、B两球相距较远，相互作用力可认为是零，A球进入水平轨道后，A、B两球间相互作用视为静电作用，带电小球均可视为质点，已知A、B两球始终没有接触，重力加速度为g。求

⑴A、B两球相距最近时，A球的速度v；

⑵A、B两球相距最近时，A、B两球系统的电势能EP；

Answer 1

【答案】（1）（2）

【解析】

（1）对A球下滑的过程，由动能定理得：2mgh＝×2mv02

v0＝
当A球进入水平轨道后，A、B两球组成的系统动量守恒，当A、B相距最近时，两球速度相等，由动量守恒定律可得：2mv0＝(2m+m)v

；
（2）由能量守恒定律得：2mgh＝(2m+m)v2+Epm

Epm=mgh