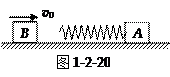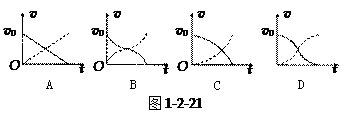题目内容
如图6-2-17所示，已知光滑水平面上有质量为M的长板正以速度v0向右运动，某时刻，质量为m的木块以与M等大的速度v0从长板右端进入长板上面向左运动，m＜M．已知木块没有滑离长板且最后木块和长板相对静止，求从木块滑上长板到木块与长板相对静止的过程中，木块和长板相对水平面的位移大小之比为多少？
=
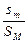由于M＞m，Mv0＞mv0，所以，最终M和m以相同的速度向右运动．即m先向左做匀减速运动，速度减到零后再向右做匀加速运动，直到和长板达到共同速度，长板一直向右做匀减速运动，直到和木块达到共同速度，之后它们一起做匀速运动．所以，木块的最小速度为零，长板的最小速度为它们一起匀速运动的速度v，由动量守恒定律得
Mv0－mv0=（M+m）v，解得v=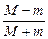
v0；
在它们相对运动的过程中，木块位移的大小为sm=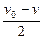
t=
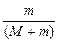v0t
长板位移大小为sM=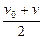
t=
v0t
它们相对水平面的位移之比为=．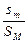
Mv0－mv0=（M+m）v，解得v=
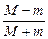v0；在它们相对运动的过程中，木块位移的大小为sm=
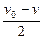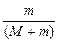t=v0t长板位移大小为sM=
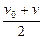t=v0t它们相对水平面的位移之比为
=．
练习册系列答案
天天向上一本好卷系列答案
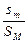小学生10分钟应用题系列答案
相关题目
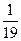m1、带电荷量为+q的金属球b用等长的绝缘轻质细线吊在天花板上，它们静止时刚好接触，并且ab接触处贴一绝缘纸、使ab碰撞过程中没有电荷转移，在PQ左侧有垂直纸面向里磁感应强度为B的匀强磁场，在PQ右侧有竖直向下的匀强电场、场强大小为E＝
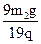。现将球b拉至细线与竖直方向成θ＝53°的位置（细线刚好拉直）自由释放，下摆后在最低点与a球发生弹性碰撞。由于电磁阻尼作用，球a将于再次碰撞前停在最低点，求经过多少次碰撞后悬挂b的细线偏离竖直方向的夹角小于37°？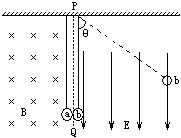
，规定向右为正方向，A、B两球的动量均为
，运动中两球发生碰撞，碰撞后A球的动量增量为
，则（ ）
A．左方是A球，碰撞后A、B两球速度大小之比为
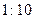
向着物块A运动，当物块B与物块A上的弹簧发生相互作用时，两物块保持在一条直线上运动．若分别用实线和虚线表示物块B和物块A的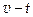
图象，则两物块在相互作用过程中，正确的
