题目内容
总质量为M的列车以匀速率v0在平直轨道上行驶，各车厢受的阻力都是车重的k倍，而与车速无关.某时刻列车后部质量为m的车厢脱钩，而机车的牵引力不变，则脱钩的车厢刚停下的瞬间，前面列车的速度是多少？
Mv0/(M－m).
此题求脱钩的车厢刚停下的瞬间，前面列车的速度，就机车来说，在车厢脱钩后，开始做匀加速直线运动，而脱钩后的车厢做匀减速运动，由此可见，求机车的速度可用匀变速直线运动公式和牛顿第二定律求解.
现在若把整个列车当作一个整体，整个列车在脱钩前后所受合外力都为零，所以整个列车动量守恒，因而可用动量守恒定律求解.
根据动量守恒定律，得：
Mv0=(M－m)V V=Mv0/(M－m)
即脱钩的车厢刚停下的瞬间，前面列车的速度为Mv0/(M－m).
现在若把整个列车当作一个整体，整个列车在脱钩前后所受合外力都为零，所以整个列车动量守恒，因而可用动量守恒定律求解.
根据动量守恒定律，得：
Mv0=(M－m)V V=Mv0/(M－m)
即脱钩的车厢刚停下的瞬间，前面列车的速度为Mv0/(M－m).
练习册系列答案
激活思维优加课堂系列答案
活力试卷系列答案
相关题目
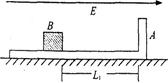多大?
