题目内容
如图所示,质量为m1、带电荷量为+q的金属球a和质量为m2=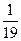 m1、带电荷量为+q的金属球b用等长的绝缘轻质细线吊在天花板上,它们静止时刚好接触,并且ab接触处贴一绝缘纸、使ab碰撞过程中没有电荷转移,在PQ左侧有垂直纸面向里磁感应强度为B的匀强磁场,在PQ右侧有竖直向下的匀强电场、场强大小为E=
m1、带电荷量为+q的金属球b用等长的绝缘轻质细线吊在天花板上,它们静止时刚好接触,并且ab接触处贴一绝缘纸、使ab碰撞过程中没有电荷转移,在PQ左侧有垂直纸面向里磁感应强度为B的匀强磁场,在PQ右侧有竖直向下的匀强电场、场强大小为E=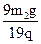 。现将球b拉至细线与竖直方向成θ=53°的位置(细线刚好拉直)自由释放,下摆后在最低点与a球发生弹性碰撞。由于电磁阻尼作用,球a将于再次碰撞前停在最低点,求经过多少次碰撞后悬挂b的细线偏离竖直方向的夹角小于37°?
。现将球b拉至细线与竖直方向成θ=53°的位置(细线刚好拉直)自由释放,下摆后在最低点与a球发生弹性碰撞。由于电磁阻尼作用,球a将于再次碰撞前停在最低点,求经过多少次碰撞后悬挂b的细线偏离竖直方向的夹角小于37°?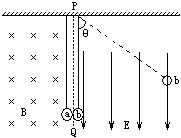
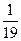 m1、带电荷量为+q的金属球b用等长的绝缘轻质细线吊在天花板上,它们静止时刚好接触,并且ab接触处贴一绝缘纸、使ab碰撞过程中没有电荷转移,在PQ左侧有垂直纸面向里磁感应强度为B的匀强磁场,在PQ右侧有竖直向下的匀强电场、场强大小为E=
m1、带电荷量为+q的金属球b用等长的绝缘轻质细线吊在天花板上,它们静止时刚好接触,并且ab接触处贴一绝缘纸、使ab碰撞过程中没有电荷转移,在PQ左侧有垂直纸面向里磁感应强度为B的匀强磁场,在PQ右侧有竖直向下的匀强电场、场强大小为E=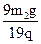 。现将球b拉至细线与竖直方向成θ=53°的位置(细线刚好拉直)自由释放,下摆后在最低点与a球发生弹性碰撞。由于电磁阻尼作用,球a将于再次碰撞前停在最低点,求经过多少次碰撞后悬挂b的细线偏离竖直方向的夹角小于37°?
。现将球b拉至细线与竖直方向成θ=53°的位置(细线刚好拉直)自由释放,下摆后在最低点与a球发生弹性碰撞。由于电磁阻尼作用,球a将于再次碰撞前停在最低点,求经过多少次碰撞后悬挂b的细线偏离竖直方向的夹角小于37°?
经过4次碰撞b球偏离竖直方向的夹角将小于37°。
设b球第一次到最低点时速度大小为V1,从自由释放到最低点的过程中,对b应用动能定理有(细线长度为L):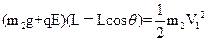 ①
①
b球从最低点(设速度为V0)运动到细线偏离竖直方向夹角φ=37°的过程中,对b应用动能定理有:
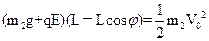 ② 即①/②得:V0=
② 即①/②得:V0=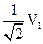 =0.707V1 ③
=0.707V1 ③
a和b在最低点发生弹性碰撞,设碰前b的速度为V,碰后a和b的速度分别为V2、V3,对a和b在碰撞过程中应用动量守恒和能量转化守恒有:m2V=m1V2+m2V3 ④
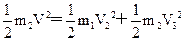 ⑤ ④⑤联立解得V3=-0.9V ⑥
⑤ ④⑤联立解得V3=-0.9V ⑥
由此可知b球碰后速度总是碰前速度的0.9倍。
ab第1次碰后b球的速度为V11=0.9 V1>V0 ⑦
ab第2次碰后b球的速度为V12=0.92 V1=0.81 V1>V0 ⑧
ab第3次碰后b球的速度为V12=0.93 V1=0.729 V1>V0 ⑨
ab第4次碰后b球的速度为V12=0.94 V1=0.6561 V1<V0 ⑩
所以经过4次碰撞b球偏离竖直方向的夹角将小于37°。
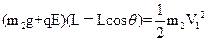 ①
① b球从最低点(设速度为V0)运动到细线偏离竖直方向夹角φ=37°的过程中,对b应用动能定理有:
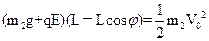 ② 即①/②得:V0=
② 即①/②得:V0=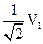 =0.707V1 ③
=0.707V1 ③ a和b在最低点发生弹性碰撞,设碰前b的速度为V,碰后a和b的速度分别为V2、V3,对a和b在碰撞过程中应用动量守恒和能量转化守恒有:m2V=m1V2+m2V3 ④
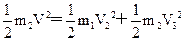 ⑤ ④⑤联立解得V3=-0.9V ⑥
⑤ ④⑤联立解得V3=-0.9V ⑥ 由此可知b球碰后速度总是碰前速度的0.9倍。
ab第1次碰后b球的速度为V11=0.9 V1>V0 ⑦
ab第2次碰后b球的速度为V12=0.92 V1=0.81 V1>V0 ⑧
ab第3次碰后b球的速度为V12=0.93 V1=0.729 V1>V0 ⑨
ab第4次碰后b球的速度为V12=0.94 V1=0.6561 V1<V0 ⑩
所以经过4次碰撞b球偏离竖直方向的夹角将小于37°。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
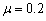 ,木板AB受到水平向左的恒力F=14N,作用一段时间后撤去,恒力F撤去时木块恰好到达弹簧自由端C处,此后运动过程中弹簧最大压缩量x = 5cm,
,木板AB受到水平向左的恒力F=14N,作用一段时间后撤去,恒力F撤去时木块恰好到达弹簧自由端C处,此后运动过程中弹簧最大压缩量x = 5cm,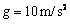 。求:
。求: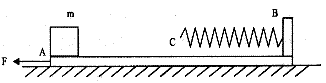



 多大?
多大?