题目内容
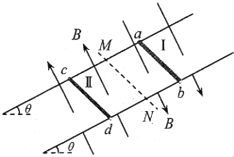
【题目】水平面内,有两根足够长的固定平行金属导轨,在它们上面横放两根平行导体棒,构成矩形回路。每根棒长度均为L,质量均为m,电阻均为R,导轨电阻不计,空间有方向竖直向下、磁感应强度为B的匀强磁场,不计电磁辐射及导体棒与导轨之间的摩擦。现已知左侧导体棒I静止,右侧导体棒II具有向右的初速度v0,如图所示,则以下判断正确的是

A. 两导体棒受到的安培力始终等大反向,整个过程中它们组成的系统动量守恒
B. 最终两导体棒将以同一速度向右做匀速运动,由于都做切割磁感线运动,电路中电流不为零
C. 从开始运动到最终达到稳定状态,整个回路产生的焦耳热为![]()
D. 从开始运动到最终达到稳定状态,两导体棒之间的距离![]() x不断增大,
x不断增大,![]() x最大值为
x最大值为![]()
【答案】ACD
【解析】A项:由于两导体棒在导轨上运动时所受的安培力等大反向,所以两棒组成的系统合外力为零,所以系统动量守恒,故A正确;
B项:最终两导体棒将以同一速度向右做匀速运动,由于穿过两棒组成的闭合回路磁通量不变,所以电路中没有电流,故B错误;
C项: 最终两导体棒的共同速度为![]() ,解得:
,解得:![]() ,由能量守恒可知,
,由能量守恒可知,![]() ,故C正确;
,故C正确;
D项:当两棒速度相等时,两棒间的距离最大,从开始运动到最终达到稳定状态,通过回路的电量为![]() ,对棒1应用动量定理可知,
,对棒1应用动量定理可知,![]() 即
即![]() ,所以
,所以![]()
由![]() 解得:
解得:![]() 即为两棒的运动距离差,所以最大距离为
即为两棒的运动距离差,所以最大距离为![]() ,故D正确。
,故D正确。

练习册系列答案
相关题目