题目内容
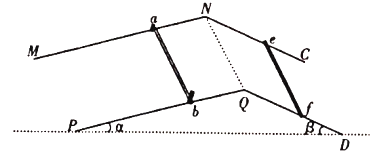
【题目】如图所示在折射n=![]() 的透明液体中水平一足够大的不透光薄板,薄板下力竖直放置着一把米尺,其零刻恰好与板上的O点重合。距离O为6cm处有一可以透光的小孔P,距离O为12cm处的Q点的正下方竖直放置着高为10cm的平面镜MN,平面镜的上端M到Q的距离为6cm。求
的透明液体中水平一足够大的不透光薄板,薄板下力竖直放置着一把米尺,其零刻恰好与板上的O点重合。距离O为6cm处有一可以透光的小孔P,距离O为12cm处的Q点的正下方竖直放置着高为10cm的平面镜MN,平面镜的上端M到Q的距离为6cm。求

(i)紧贴着液面的人能够直接观察到米尺的刻度范围;
(ii)通过平面镜人能够观察到米尺的刻度范围。
【答案】(1)8cm~100cm(2)24cm~48cm
【解析】
作出刻度尺通平面镜的成像光路图,米尺上的B点发出的光线,经过平面镜反射从P点射向液面时,刚好发生全反射,B点即为人观察到米尺的上边界,结合几何关系解题。
(1)如图所示,
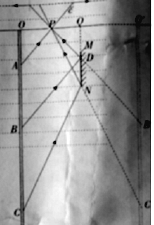
米尺上的A点发出的光线,经过P点射向液面时,刚好发生全反射,A点即为人观察到米尺的上边界。
根据折射定律,液体的临界角满足
![]()
由几何关系得:
![]()
解得:![]()
显然,人观察到米尺的下边界为米尺的末端100cm;
(2)作出刻度尺通平面镜的成像光路图,米尺上的B点发出的光线,经过平面镜反射从P点射向液面时,刚好发生全反射,B点即为人观察到米尺的上边界。
由几何关系
![]()
解得:![]()
米尺上的C点发出的光,经过平面镜的下边界反射从P点射向液面,可以被人观察到,C点即为人观察到米尺的下边界
由几何关系得:
![]()
解得:![]()
通过平面镜,人能观察到米尺的范围为24cm![]() 48cm。
48cm。

练习册系列答案
相关题目