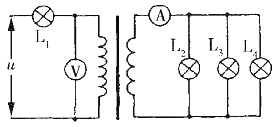
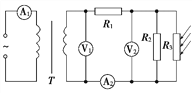
��Ŀ����
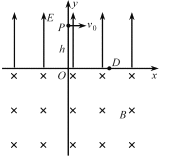
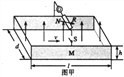
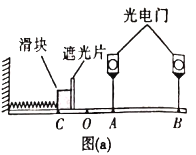
����Ŀ����ͼ��ʾ�㹻���Ľ�������MNC��PQDƽ���Ҽ��ΪL������ƽ����ˮƽ��нǷֱ�Ϊ��=37������=53����������ռ���д�ֱ����ƽ�����µ���ǿ�ų�(ͼ��δ����)���Ÿ�Ӧǿ�ȴ�СΪB�����Ƚ�����ab��ef������Ϊm������ΪL�������ΪR���˶������У����������뵼�챣�����ýӴ�ʼ�մ�ֱ�ڵ��죬������ef�뵼���Ķ�Ħ������Ϊ��=0.5��������ab�⻬��������費���������ٶȴ�СΪg��sin37��=0.6��co837��=0.8��
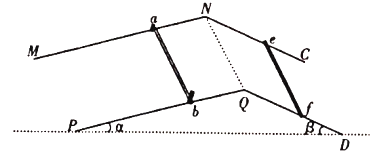
(1)������ab��������ֹ�ͷŰ�ef�����ef�����˶����ٶ�v1��
(2)����ef����ʱ��t�ﵽ��(1)���е��ٶ�v1����˹����а�ef�»��ľ���x��
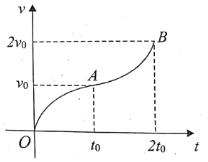
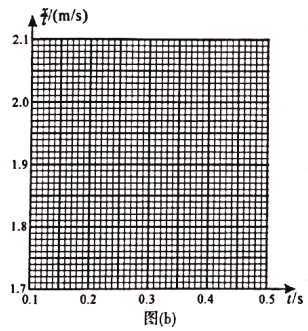
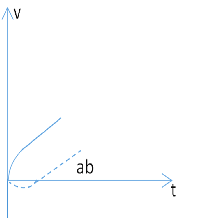
(3)�������������⻬��ͬʱ�ɾ�ֹ�ͷţ�����ͬһͼ�ж��Ի��������˶���v��tͼ�ߡ�(ab��ȡ�ع�������˶�Ϊ������ef��ȡ�ع�������˶�Ϊ������)
���𰸡�(1)![]() (2)
(2)![]() (3)
(3) 
��������
�ɼ���֪ʶ�����·������仯��������ζ��ɺ�ŷķ���ɣ�����ͨ��ab��ij�����ĵ����������ݷ����ڵ�Ÿ�Ӧ���ɼ���綯�ƵĴ�С�����ݰ�������������ǿ�ų��ĴŸ�Ӧǿ����⡣
(1)��ef���������˶�����ef��������
������ƽ�������У�
![]()
�ɰ�������ʽ�ã�
![]()
��ŷķ���ɵã�![]()
�ɷ����ڵ�Ÿ�Ӧ���ɵã�
![]()
������ã�![]() ��
��
(2)��ef�ɾ�ֹ���ٶ�Ϊ![]() ��������ʱ��Ϊt��λ��Ϊx����ef���ɶ��������ã�
��������ʱ��Ϊt��λ��Ϊx����ef���ɶ��������ã�
![]()
�ɱպϵ�·ŷķ�����У�![]()
�ɷ����ڵ�Ÿ�Ӧ�����У�![]()
��·��ͨ���ı仯Ϊ��![]()
������ã�![]() ��
��
(3)����ef�ع���ȼ����»�����ab�ع���ȼ����ϻ������ٶ���ͬ����v-tͼ������