��Ŀ����
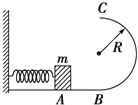
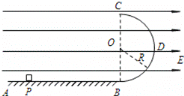
����Ŀ����ͼ��ʾ����Եˮƽ���������ΪL=15m��A��B���㣬����Ϊm=2.2kg��������Ϊq=+3��10��4C�����徲ֹ����ˮƽ���ϵ�A�㣬����ˮƽ���Ķ�Ħ������Ϊ��=0.5��ijʱ�̣��ռ������ˮƽ�������=37����б���ϵ���ǿ�糡��ʹ����Ӿ�ֹ��ʼ�����˶�������C��ʱ���糡ͻȻ��ʧ����������˶���Bλ��ͣ�¡���֪��������˶���ʱ���Ǽ����˶�ʱ���2����sin37��=0.6��cos37��=0.8���������ٶ�gȡ10m/s2����
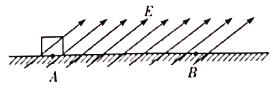
(1)��ǿ�糡�ĵ糡ǿ�ȣ�
(2)�糡��A��C����֮��ĵ��Ʋ
���𰸡���1��![]() ��2��
��2��![]()
��������
��1�������ȼ��ٺ���٣������˶���ʽ�����ٽεļ��ٶȣ����ţ�ٵڶ�������ⳡǿ�Ĵ�С����2�������ٽεľ��룬����U=Ed�����Ʋ�.
��1����糡��ΪF��AC��BC����ٶȡ�ʱ��ֱ�Ϊa��a����t��t�����������֪���������ȼ����˶��ļ��ٶ�Ϊ![]()
�����ȼ��ٽε�ĩ�ٶȼ�Ϊ�ȼ��ٽεij��ٶȣ����at=a��t��
��t��=2t
���a=2a��=10m/s2��
�����ڵ糡�����������ȼ����˶�����ţ�ٵڶ����ɣ�![]() ���F=30N��
���F=30N��
��糡ǿ��![]()
��2�������A�˶���B,�У�![]() ��t��=2t��
��t��=2t��
����ٽε�λ�ƣ�![]()
AC����֮��ĵ��Ʋ�![]()

��ϰ��ϵ�д�
 �Űٷֿ�ʱ����ϵ�д�
�Űٷֿ�ʱ����ϵ�д� ������״Ԫ��ҵϵ�д�
������״Ԫ��ҵϵ�д�
�����Ŀ