��Ŀ����
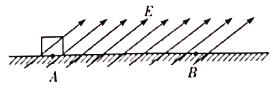
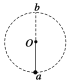
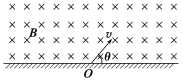
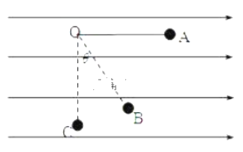
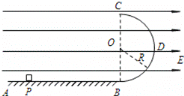
����Ŀ����ͼ��ʾ��ˮƽ��Ե���AB�봦����ֱƽ���ڵİ�Բ�ξ�Ե�⻬���BCƽ�����ӣ���Բ�ι���İ뾶R=0.40m��������ڿռ����ˮƽ���ҵ���ǿ�糡���糡ǿ��E=1.0��104 N/C������һ�����q=+1.0��10��4C������m=0.10kg�Ĵ����壨����Ϊ�ʵ㣩����ˮƽ����ϵ�P���ɾ�ֹ�ͷţ��������˶���Բ�ι����͵�Bʱ���ٶ�vB=5.0m/s����֪��������ˮƽ�����Ķ�Ħ��������=0.50���������ٶ�g=10m/s2����
��1���������˶���Բ�ι������͵�Bʱ���������Բ�ι����ѹ����
��2����������ˮƽ����ϵ��ͷŵ�P��B��ľ��룻
��3���������һ�ξ���C�������ˮƽ����ϵ�λ�õ�B��ľ��룮
���𰸡�(1) 7.25N��������ֱ���� (2) 2.5m (3) 0.40m
��������
��1�����������B���ܵ���֧����ΪFN����ţ�ٵڶ����ɵã�
FN��mg=m![]()
��ã�
FN=7. 25N
����ţ�ٵ������ɣ�F��N= FN=7.25N��������ֱ����
��2����PB��ľ���Ϊs�����ڶ��ܶ����ã�
��qE����mg��s=![]() mvB2��0
mvB2��0
��ã�
s=2.5m
��3����������˶���C����ٶ�ΪvC���ɶ��ܶ����ã�
![]()
�������뿪C�������ֱ�����������������˶�
2R=![]() gt2
gt2
��ˮƽ���������ȼ����˶�������ˮƽ����ļ��ٶȴ�СΪa������ţ�ٵڶ����ɣ�
qE=ma
������ˮƽ����ϵ�λ�õ�B��ľ���Ϊx��ˮƽ����λ�ƣ�
x=vct��![]() at2
at2
��ã�
x=0.40m��

 �»����ܶ�Ա��ϵ�д�
�»����ܶ�Ա��ϵ�д� ����ͼ����ּ��������ҵ֣�ݴ�ѧ������ϵ�д�
����ͼ����ּ��������ҵ֣�ݴ�ѧ������ϵ�д�