题目内容
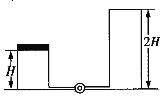
【题目】如图所示，AB是一段长为s的光滑绝缘水平轨道，BC是一段竖直墙面。一带电量为q(q>0)的小球静止在A点。某时刻在整个空间加上水平向右、场强E=
的匀强电场，当小球运动至B点时，电场立即反向(大小不变)，经一段时间后，小球第一次运动至C点。重力加速度为g。求：
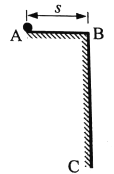
（1）小球由A运动至B的时间t；
（2）竖直墙面BC的高度h；
（3）小球从B点抛出后，经多长时间动能最小?最小动能是多少?
【答案】（1）
（2）
（3）
【解析】
根据“小球在匀强电场中运动至B点，经一段时间后小球第一次运动至C点”可知，本题考查带电小球在匀强电场中的曲线运动问题，根据匀变速曲线运动的运动规律，运用动能定理和分运动的运动学公式列式计算.
(1)小球由A至B，由牛顿第二定律得：
位移为
联立解得运动时间：
(2)设小球运动至B时速度为vB，则
小球由B运动至C的过程中，在水平方向做加速度为-a的匀变速运动，位移为0，
则：
在竖直方向上做自由落体运动，则
联立解得：
(3)从B点抛出后经时间t，水平方向、竖直方向速度分别为
经时间t合速度v满足
代入得：
由此，当
时，
最小，最小值
，
故小球从B点抛出后，达动能最小需经时间
动能最小值
练习册系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
