题目内容
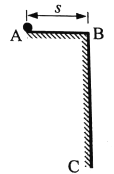
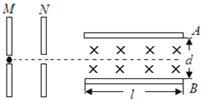
【题目】如图所示,A、B为一对平行板,板长为l,两板距离为d,板间区域内充满着匀强磁场,磁感应强度大小为B,方向垂直纸面向里,一个质量为m,带电量为+q的带电粒子自静止开始经M、N两平行金属板间的电场加速后,从A、B两板的中间沿垂直于磁感线的方向射入磁场.(不计粒子的重力)求:
(1)若粒子被加速后进入磁场的速度为v0,则它在磁场中做圆周运动的半径和周期各为多少?
(2)MN两极板间的电压U应在什么范围内,粒子才能从磁场内射出?
【答案】(1)![]() ,
,![]() (2)
(2)![]() 或
或![]()
【解析】
(1)“由粒子从A、B两板的中间沿垂直于磁感线的方向射入磁场”可知,本题考查了带电粒子在匀强磁场中做圆周运动。由由洛伦兹力提供向心力,由牛顿第二定律求出半径,由圆周运动的周期公式求解周期.
(2)由“粒子才能从磁场内射出”可知,本题考查了带电粒子在匀强磁场中运动的临界条件。当粒子从平行板左边射出时,最大半径为r1![]() ,粒子从左边射出必须满足r≤r1.当粒子恰好从平行板右边射出时,由几何知识半径r2,即为粒子从右边射出时运动轨迹最小半径.由半径公式和动能定理求解电压的范围.
,粒子从左边射出必须满足r≤r1.当粒子恰好从平行板右边射出时,由几何知识半径r2,即为粒子从右边射出时运动轨迹最小半径.由半径公式和动能定理求解电压的范围.
(1)粒子在磁场做圆周运动的向心力由洛伦兹力提供,则有:qv0B=m![]()
解得:r![]() ; 周期T
; 周期T![]() .
.
(2)带电粒子在MN两极板间的加速过程由动能定理得:qU![]()
如图所示,当粒子从左边射出时,若运动轨迹半径最大
其圆心为图中O1点,半径r1![]() .因此粒子从左边射出必须满足r≤r1
.因此粒子从左边射出必须满足r≤r1
联立解得:U![]() .
.
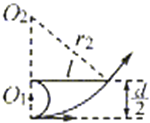
当粒子从右边射出时,若运动轨迹半径最小,则其圆心为图中O2点,设半径为r2.
由几何关系可得:![]()
解得 ![]()
因此粒子从右边射出必须满足的条件是:r≥r2
联立解得:U![]()

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目