��Ŀ����
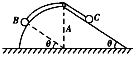
����Ŀ�������˶��������˷dz�ϲ�����˶�����ͼ��ʾ��BC��Բ������Ӧ��Բ��ΪO�㣬Բ�Ľ�Ϊ60�����뾶OC��ˮƽ���CD��ֱ��ˮƽ���CD�δֲڣ�����sCD=8m��һ�˶�Ա��A����v0=3m/s���ٶ�ˮƽ��������B��պ��ع�������߷�����⻬Բ���ι��BC�������CD����Ϲ⻬���DE,����E��ʱ�ٶȼ�Ϊ�㣬Ȼ�ء��˶�Ա�ͻ����������Ϊm��B��E�����ˮƽ���CD����ֱ�߶ȷֱ�Ϊh��H����h=2m,H=2.8m,gȡ10m/s2.��
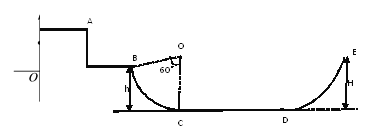
��1�����˶�Ա��A���˶���B��ʱ���ٶȴ�СvB��
��2������CD�뻬���Ķ�Ħ����������
��3��ͨ������˵������һ�η���ʱ���˶�Ա�ܷ�ص�B�㣿����ܣ�������˶�Ա�ص�B���ǵ��ٶȴ�С��������ܣ�������˶�Աͣ�ںδ���
���𰸡���1��![]() ��2��
��2��![]() ��3��
��3��![]() ��
��![]()
��������
��1���������֪��
![]() ����
����
��ã�
vB=2v0=6m/s
��2����B�㵽E�㣬�ɶ��ܶ����ɵã�
![]() ����
����
�ɢ٢ڴ������ݿɵã�
��=0.125
��3���˶�Ա�ܵ����������߶�Ϊh'����B����һ�η��������ߴ������ݶ��ܶ����У�![]()
��ã�
h'=1.8m��h=2m
���Ե�һ�η���ʱ���˶�Ա���ܻص�B�㣻
���˶�Ա��B���˶���ֹͣ����CD�ε���·��ΪS���ɶ��ܶ����ɵã�
![]() ����
����
�������ݽ�ã�
S=30.4m
��ΪS=3SCD+6.4m�������˶�Ա���ͣ��D�����6.4m������C���Ҳ�1.6m����

 ���Ž�������С״Ԫϵ�д�
���Ž�������С״Ԫϵ�д�