题目内容
（18分）如图所示，粗糙斜面与光滑水平面通过半径可忽略的光滑小圆弧平滑连接，斜面倾角α=37°，A、B、Ｃ是三个质量均为 m=1㎏的小滑块（可视为质点），C为左端附有胶泥（胶泥的质量不计），D为两端分别连接B和C的轻质弹簧．弹簧和滑块B、Ｃ均处于静止状态．
（1）．当滑块A置于斜面上且受到大小F=4N，方向垂直斜面向下的恒力作用时，恰能向下匀速运动．求滑块A斜面之间的动摩擦因数
。
（2）．现撤去F，让滑块A从斜面上距斜面底端L=1m处由静止下滑，若取g=10m/s2，sin37°=0.6，cos37°=0.8．求滑块A到达斜面底端时的速度大小
。
（3）．滑块A与C接触后粘连在一起，求此后滑块和弹簧构成的系统在相互作用过程中，弹簧的最大弹性势能Ep．
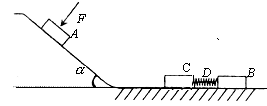
（18分）
解析：（18分）(1)滑块
匀速下滑时，受重力mg、恒力F、斜面支持力FN和摩擦力Fμ作用，
由平衡条件有 
（2分）
即
（３分）
化简后得
，代入数据解得动摩擦因数
（1分）
（2）撤去
后，滑块匀加速下滑，由动能定理有
（3分）
代入数据得
（1分）
（3）滑块A、C粘接后瞬间共同速度为
（２分），
滑块和弹簧构成的系统在相互作用过程中动量守恒，当它们速度相等时，弹簧具有最大弹性势能，设共同速度为
，由动量守恒和能量守恒定律有
（２分）
（3分）
联立解得 
（１分）
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
（2005?新洲区模拟）如图所示，粗糙斜面与光滑水平面通过半径可忽略的光滑小圆弧平滑连接，斜面倾角α=37°，A、B是两个质量均为m=1kg的小滑块（可看作质点），C为左端附有胶泥的质量不计的薄板，D为两端分别连接B和C的轻质弹簧．当滑块A置于斜面上且受到大小F=4N，方向垂直斜面向下的恒力作用时，恰能向下匀速运动．现撤去F，让滑块A从斜面上距斜面底端L=1m处由静止下滑．（g=10m/s2，sin37°=0.6，cos37°=0.8）
（2013?辽宁一模）如图所示，粗糙斜面与水平面通过半径可忽略的光滑小圆弧平滑连接，斜面倾角α=37°，水平面的M到N段是长度L1=0.3m的粗糙平面，N点的右边是光滑的．A、B是两个质量均为m=1kg的小滑块（可看作质点），置于N点处的C是左端附有胶泥的薄板（质量不计），D是两端分别与B和C连接的轻质弹簧，滑块A与斜面和与水平面MN段的动摩擦因数相同．当滑块A置于斜面上且受到大小F=4N、方向垂直斜面向下的恒力作用时，恰能向下匀速运动．现撤去F，让滑块A从斜面上距斜面底端L2=1m处由静止下滑（取g=10m/s2，sin37°=0.6，cos37°=0.8），求：滑块A与C接触并粘连在一起后，两滑块与弹簧所构成的系统在相互作用的过程中，弹簧的最大弹性势能．
如图所示，粗糙斜面与光滑水平面通过半径可忽略的光滑小圆弧平滑连接，斜面倾a=37°，A、B、C是三个小滑块（可看做质点），A、B的质量均为m=1kg，B的左端附有胶泥（质量不计），C的质量均为M=2kg，D为两端分别连接B和C的轻质弹簧．