题目内容
 (2013?辽宁一模)如图所示,粗糙斜面与水平面通过半径可忽略的光滑小圆弧平滑连接,斜面倾角α=37°,水平面的M到N段是长度L1=0.3m的粗糙平面,N点的右边是光滑的.A、B是两个质量均为m=1kg的小滑块(可看作质点),置于N点处的C是左端附有胶泥的薄板(质量不计),D是两端分别与B和C连接的轻质弹簧,滑块A与斜面和与水平面MN段的动摩擦因数相同.当滑块A置于斜面上且受到大小F=4N、方向垂直斜面向下的恒力作用时,恰能向下匀速运动.现撤去F,让滑块A从斜面上距斜面底端L2=1m处由静止下滑(取g=10m/s2,sin37°=0.6,cos37°=0.8),求:滑块A与C接触并粘连在一起后,两滑块与弹簧所构成的系统在相互作用的过程中,弹簧的最大弹性势能.
(2013?辽宁一模)如图所示,粗糙斜面与水平面通过半径可忽略的光滑小圆弧平滑连接,斜面倾角α=37°,水平面的M到N段是长度L1=0.3m的粗糙平面,N点的右边是光滑的.A、B是两个质量均为m=1kg的小滑块(可看作质点),置于N点处的C是左端附有胶泥的薄板(质量不计),D是两端分别与B和C连接的轻质弹簧,滑块A与斜面和与水平面MN段的动摩擦因数相同.当滑块A置于斜面上且受到大小F=4N、方向垂直斜面向下的恒力作用时,恰能向下匀速运动.现撤去F,让滑块A从斜面上距斜面底端L2=1m处由静止下滑(取g=10m/s2,sin37°=0.6,cos37°=0.8),求:滑块A与C接触并粘连在一起后,两滑块与弹簧所构成的系统在相互作用的过程中,弹簧的最大弹性势能.分析:滑块A匀速下滑时,合力为零,分析受力情况,由平衡条件求解动摩擦因数;撤去F后,滑块A做匀加速运动,根据动能定理求出滑块A滑到斜面底端时的速度大小,两滑块和弹簧构成的系统在相互作用过程中动量守恒,当它们速度相等时,弹簧具有最大弹性势能,根据系统的动量守恒和机械能守恒求解弹簧的最大弹性势能.
解答:解:(1)设滑块A与斜面和与水平面MN段的动摩擦因数均为μ,施加恒力时根据平衡条件得:
μ(F+mgcosα)=mgsinα
未施加力时,设A滑到斜面底端的速度然后,滑块在MN段运动时,受水平面的摩擦力作用速度减为v2,由动能定理有:
(mgsinα-μmgcosα)L2-μmgL1=
mv12
代入数据得:v2=1m/s
滑块A与C接触后,A、B、C、D组成的系统动量守恒,能量守恒,所以当A、B具有共同速度v3时,系统的动能最小,弹簧弹性势能最大,设为Ep,则:
mv2=2mv3
mv22=Ep+
×2mv32
代入数据得:Ep=0.25J
答:滑块A与C接触并粘连在一起后,两滑块与弹簧所构成的系统在相互作用的过程中,弹簧的最大弹性势能为0.25J.
μ(F+mgcosα)=mgsinα
未施加力时,设A滑到斜面底端的速度然后,滑块在MN段运动时,受水平面的摩擦力作用速度减为v2,由动能定理有:
(mgsinα-μmgcosα)L2-μmgL1=
| 1 |
| 2 |
代入数据得:v2=1m/s
滑块A与C接触后,A、B、C、D组成的系统动量守恒,能量守恒,所以当A、B具有共同速度v3时,系统的动能最小,弹簧弹性势能最大,设为Ep,则:
mv2=2mv3
| 1 |
| 2 |
| 1 |
| 2 |
代入数据得:Ep=0.25J
答:滑块A与C接触并粘连在一起后,两滑块与弹簧所构成的系统在相互作用的过程中,弹簧的最大弹性势能为0.25J.
点评:本题是平衡条件和动能定理的综合应用,按程序法进行分析研究,抓住弹簧具有最大弹性势能时,两滑块的速度相等这个临界条件是解题的关键.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
 (2013?辽宁一模)我国国家大剧院外部呈椭球形.假设国家大剧院的屋顶为半球形,一警卫人员为执行特殊任务,必须冒险在半球形屋顶向上缓慢爬行,他在向上爬的过程中( )
(2013?辽宁一模)我国国家大剧院外部呈椭球形.假设国家大剧院的屋顶为半球形,一警卫人员为执行特殊任务,必须冒险在半球形屋顶向上缓慢爬行,他在向上爬的过程中( )
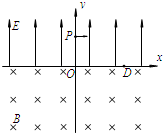 (2013?辽宁一模)在如图所示的xoy坐标系中,y>0的区域内存在着沿y轴正方向、场强为E的匀强电场,y<0的区域内存在着垂直纸面向里、磁感应强度为B的匀强磁场.一带电粒子从y轴上的P(0,h)点以沿x轴正方向的初速度射出,恰好能通过x轴上的D(d,0)点.已知带电粒子的质量为m,带电量为-q.h、d、q均大于0,不计重力的影响.
(2013?辽宁一模)在如图所示的xoy坐标系中,y>0的区域内存在着沿y轴正方向、场强为E的匀强电场,y<0的区域内存在着垂直纸面向里、磁感应强度为B的匀强磁场.一带电粒子从y轴上的P(0,h)点以沿x轴正方向的初速度射出,恰好能通过x轴上的D(d,0)点.已知带电粒子的质量为m,带电量为-q.h、d、q均大于0,不计重力的影响.