题目内容
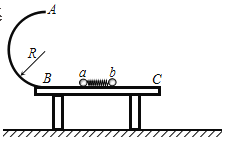
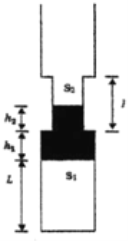
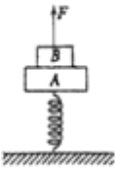
【题目】如图所示，一轻质弹簧的下端固定在水平面上，上端叠放两个质量均为M的物体
（A 物体与弹簧连接），弹簧的劲度系数为k，初始时物体处于静止状态。现用竖直向上的拉 力F作用在物体B上，使物体
开始向上一起做加速度为a的匀加速运动直到 分离，重力加速度为g，其中
，则
A. 外力施加的瞬间，间的弹力大小为
B. 
刚分离时，弹簧弹力恰好为零
C. 分离时，
上升的高度为
D. A. B分离后，A速度最大时弹簧恰好恢复原长
【答案】A
【解析】
A.拉力F施加的瞬间，对A物体，根据牛顿第二定律有：
F弹-Mg-FAB=Ma
F弹=2Mg
解得：
FAB=M（g-a）
故A正确.
BC.两物体处于初始静止状态时，对AB整体受力分析得：
2Mg=kx0
此时弹簧的压缩量为：
在AB分离瞬间，AB间的弹力FAB=0，弹簧弹力不为零，对A受力分析得：
kx-Mg=Ma
得到这一瞬间弹簧的压缩量为
故BC错误.
D.在物体A上升的过程，当A物体的重力Mg和弹簧弹力相等时，其速度最大.故D错误.
练习册系列答案
相关题目
