题目内容
【题目】如图所示,一带负电的点电荷固定于O点,电荷量Q=5×10-6C,其右侧竖直放置光滑绝缘细杆,杆上AB两点高度差为h=0.4m,B点与O点等高且OB距离d=0.3m。另有一个穿过细杆可视为点电荷的带正电小球,其质量m=6×10-3kg、电荷量为q=5×10-8C.现将小球从A点由静止开始释放,小球向下运动至B点时,速度v=3m/s。已知静电力常量为k=9×109N·m2/C2,重力加速度g=10m/s2,不计空气阻力.求:
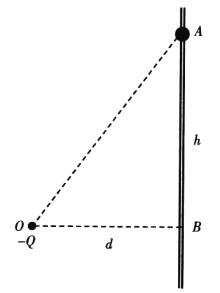
(1)小球在A点释放瞬间的加速度大小
(2)A、B间的电势差UAB.
【答案】(1)a=11.2m/s2 (2)UAB=6×104V
【解析】
(1)根据库仑定律求解小球在A点受到的库仑力,对小球根据牛顿第二定律求解加速度大小;
(2)小球从A到B根据动能定理求解电势差.
(1)根据几何关系可知,A点距离O点的距离为:![]()
小球在A点受到的库仑力为: ![]()
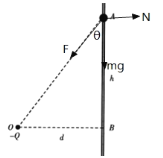
设OA和AB的夹角为θ,则有: ![]()
则有:θ=37°
对小球根据牛顿第二定律可得:Fcosθ+mg=ma
联立并代入数据解得:a=11.2m/s2;
(2)小球从A到B根据动能定理可得:![]()
由于WAB=qUAB
代入数据解得:UAB=6×104V

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目