题目内容
14.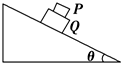 如图所示,质量分别为m和M的两物体P和Q叠放在倾角为θ的斜面上,P、Q之间的动摩擦因数为μ1,Q与斜面间的动摩擦因数为μ2.当它们从静止开始沿斜面下滑时,两物体始终保持相对静止,则
如图所示,质量分别为m和M的两物体P和Q叠放在倾角为θ的斜面上,P、Q之间的动摩擦因数为μ1,Q与斜面间的动摩擦因数为μ2.当它们从静止开始沿斜面下滑时,两物体始终保持相对静止,则(1)斜面对Q的摩擦力大小为多少?
(2)物体P受到的摩擦力大小为多少?
分析 (1)根据滑动摩擦力公式可以求出斜面对Q的摩擦力大小;
(2)先对PQ整体受力分析,根据牛顿第二定律求解出加速度,然后隔离出物体P,受力分析后根据牛顿第二定律列式求解出间的静摩擦力.
解答 解:(1)Q受到斜面的滑动摩擦力:f=μ2(m+M)gcosθ;
(2)P、Q系统受力如图所示,由牛顿第二定律得:
(M+m)gsinθ-fQ=(M+m)a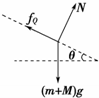
N=(m+M)gcosθ,其中:fQ=μ2N,
解得,加速度:a=gsinθ-μ2gcosθ,
对物体P,设P受到的静摩擦力为fP,方向沿斜面向上,
对P,由牛顿第二定律得:mgsinθ-fP=ma,
解得:fP=μ2mgcosθ.
答:(1)斜面对Q的摩擦力大小为μ2(m+M)gcosθ;
(2)物体P受到的摩擦力大小为μ2mgcosθ.
点评 本题关键是先对整体受力分析,根据牛顿第二定律求解出加速度,然后再隔离出物体P,运用牛顿第二定律求解PQ间的作用力.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
2.人类对落体运动的认识经历了差不多两千年的时间口下列有关落体运动的说法正确的有( )
| A. | 亚里士多德认为物体下落的快慢由其物重决定 | |
| B. | 如果完全排除空气的阻力,落体运动就成为自由落体运动 | |
| C. | 考虑空气阻力的影响,较轻的物体下落的快一些 | |
| D. | 伽利略在研究落体运动时用到了理想斜面实验 |
19. 在竖直墙壁间有质量为m、倾角为30°的直角楔形木块和质量为2m的光滑圆球,两者能够一起以加速度a匀加速竖直下滑,已知a<g (g为重力加速度).则木块与左侧墙壁之间的动摩擦因数为( )
在竖直墙壁间有质量为m、倾角为30°的直角楔形木块和质量为2m的光滑圆球,两者能够一起以加速度a匀加速竖直下滑,已知a<g (g为重力加速度).则木块与左侧墙壁之间的动摩擦因数为( )
 在竖直墙壁间有质量为m、倾角为30°的直角楔形木块和质量为2m的光滑圆球,两者能够一起以加速度a匀加速竖直下滑,已知a<g (g为重力加速度).则木块与左侧墙壁之间的动摩擦因数为( )
在竖直墙壁间有质量为m、倾角为30°的直角楔形木块和质量为2m的光滑圆球,两者能够一起以加速度a匀加速竖直下滑,已知a<g (g为重力加速度).则木块与左侧墙壁之间的动摩擦因数为( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
6.如图所示,带箭头的直线是某一电场中的一条电场线,在这条线上有A、B两点,则( )


| A. | 电场线从A指向B,所以EA>EB | |
| B. | 因为A、B在一条电场上,且电场线是直线,所以EA=EB | |
| C. | A点电势比B点电势高 | |
| D. | 不知A、B附近电场线的分布情况,所以不能比较电场强度大小和电势高低 |
4. 如图所示,真空中四个点电荷分别位于边长为L 的立方体的四个顶点上,电荷量分别为+q和-q(q>0),a、b 分别为立方体上、下面的对角线交点,c为线段ab的中点.下列说法中正确的是( )
如图所示,真空中四个点电荷分别位于边长为L 的立方体的四个顶点上,电荷量分别为+q和-q(q>0),a、b 分别为立方体上、下面的对角线交点,c为线段ab的中点.下列说法中正确的是( )
 如图所示,真空中四个点电荷分别位于边长为L 的立方体的四个顶点上,电荷量分别为+q和-q(q>0),a、b 分别为立方体上、下面的对角线交点,c为线段ab的中点.下列说法中正确的是( )
如图所示,真空中四个点电荷分别位于边长为L 的立方体的四个顶点上,电荷量分别为+q和-q(q>0),a、b 分别为立方体上、下面的对角线交点,c为线段ab的中点.下列说法中正确的是( )| A. | a、b 两点的电场强度相同 | |
| B. | a、b、c 三点的电场强度方向相同 | |
| C. | 让某检验电荷从a 点沿ab 移到b 点,其电势能不变 | |
| D. | 让某检验电荷从a 点沿ab 移到b 点,其所受电场力大小先变大后变小 |
 如图所示,光滑水平面AB与竖直面内的半圆形导轨在B点衔接,导轨半径为R,一个质量为m的物块以某一速度向右运动,当它经过B点进入导轨瞬间对导轨的压力为其重力的7倍,而后向上运动恰能完成半圆周运动到C点,求:
如图所示,光滑水平面AB与竖直面内的半圆形导轨在B点衔接,导轨半径为R,一个质量为m的物块以某一速度向右运动,当它经过B点进入导轨瞬间对导轨的压力为其重力的7倍,而后向上运动恰能完成半圆周运动到C点,求: