题目内容
4. 如图所示,光滑水平面AB与竖直面内的半圆形导轨在B点衔接,导轨半径为R,一个质量为m的物块以某一速度向右运动,当它经过B点进入导轨瞬间对导轨的压力为其重力的7倍,而后向上运动恰能完成半圆周运动到C点,求:
如图所示,光滑水平面AB与竖直面内的半圆形导轨在B点衔接,导轨半径为R,一个质量为m的物块以某一速度向右运动,当它经过B点进入导轨瞬间对导轨的压力为其重力的7倍,而后向上运动恰能完成半圆周运动到C点,求:(1)物块在B点时的动能为多少?
(2)物块在C点时的动能为多少?
(3)物块从B到C点过程中阻力所做的功为多少?
分析 研究物体经过B点的状态,根据牛顿运动定律求出物体经过B点的速度,物体恰好到达C点时,由重力充当向心力,由牛顿第二定律求出C点的速度,物体从B到C的过程,运用动能定理求解克服阻力做的功
解答 解:物块运动到B点,
由于其对导轨的压力为其重力的7倍,
故有:7mg-mg=m$\frac{{v}_{B}^{2}}{R}$,
B点物体的动能为EkB=$\frac{1}{2}$mv${v}_{B}^{2}$=3mgR,
物块恰好过C点有:mg=m$\frac{{v}_{C}^{2}}{R}$,
C点的动能EkC=$\frac{1}{2}$mgR.
设物块克服阻力做功为Wf,
物块从B点到C点运用动能定理有:-mg•2R-Wf=EkC-EkB=-$\frac{5}{2}$mgR,
故物块从B点到C点阻力所做的功Wf=-$\frac{1}{2}$mgR.
答:(1)物块在B点时的动能为3mgR
(2)物块在C点时的动能为$\frac{1}{2}mgR$
(3)物块从B到C点过程中阻力所做的功为-$\frac{1}{2}mgR$
点评 本题的解题关键是根据牛顿第二定律求出物体经过B、C两点的速度,再结合动能定理求解,难度适中

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
6.下列说法中正确的是( )
| A. | 动量守恒定律是由牛顿运动定律推导出来的,所以不能用于研究微观粒子 | |
| B. | 一个氢原子从n=3的激发态跃迁到基态时,最多能辐射3种不同频率的光子 | |
| C. | 天然放射现象的发现揭示了原子核还可再分 | |
| D. | 用γ射线治疗肿瘤时一定要严格控制剂量,以免对人体正常组织造成太大的伤害 |
15.下列说法正确的是( )
| A. | 一定量的某种气体,在对外做功时,其内能可能不变 | |
| B. | 给篮球打气时,到后来越来越费劲,说明分子间存在斥力 | |
| C. | 液体表面层的分子较稀疏,分子间引力大于斥力,因此产生液体的表面张力 | |
| D. | 液晶既有液体的流动性,又有晶体的各向异性 | |
| E. | 第二类永动机能制造出来,因为它违反热力学第一定律 |
9.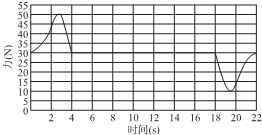 在电梯中,把一重物置于水平台秤上,台秤与力的传感器相连,电梯从静止开始一直上升,最后停止运动:传感器的屏幕上显示出其所受的压力与时间的关系(FN一t)图象,如图所示,则下列说法中正确的是( )
在电梯中,把一重物置于水平台秤上,台秤与力的传感器相连,电梯从静止开始一直上升,最后停止运动:传感器的屏幕上显示出其所受的压力与时间的关系(FN一t)图象,如图所示,则下列说法中正确的是( )
 在电梯中,把一重物置于水平台秤上,台秤与力的传感器相连,电梯从静止开始一直上升,最后停止运动:传感器的屏幕上显示出其所受的压力与时间的关系(FN一t)图象,如图所示,则下列说法中正确的是( )
在电梯中,把一重物置于水平台秤上,台秤与力的传感器相连,电梯从静止开始一直上升,最后停止运动:传感器的屏幕上显示出其所受的压力与时间的关系(FN一t)图象,如图所示,则下列说法中正确的是( )| A. | 0~4s电梯中的物体处于超重状态 | |
| B. | 18~22s内,电梯中的物体处于先超重再失重状态 | |
| C. | 从图中可以求出物体的重力 | |
| D. | 从图中可以找出电梯上升时最大加速度 |
13.某同学在“用打点计时器测速度”的实验中,用打点计时器记录了被小车拖动的纸带的运动情况(图1),在纸带上确定出A,B,C,D,E,F,G共7个计数点.其相邻点间的距离如图1所示,每两个相邻的测量点之间的时间间隔为0,10s.
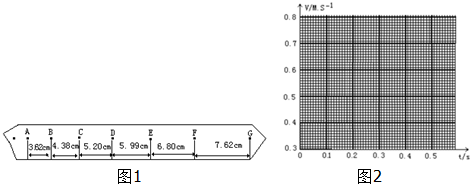
(1)试根据图1纸带上各个计数点间的距离,每个0.10s测一次速度,计算出打下C点时小车的瞬时速度,并将速度值填入表格(要求保留2位有效数字);
(2)将B、C、D、E、F各个时刻的瞬时速度标在图2直角坐标系中,并画出小车的瞬时速度随时间变化的关系图线并算出小车的加速度a=0.80m/s2.

(1)试根据图1纸带上各个计数点间的距离,每个0.10s测一次速度,计算出打下C点时小车的瞬时速度,并将速度值填入表格(要求保留2位有效数字);
| VB | VC | VD | VE | VF | |
| 数值(m/s) | 0.40 | 0.48 | 0.56 | 0.64 | 0.72 |
 在“探究单摆摆长与周期关系”的实验中,某同学的主要操作步骤如下:
在“探究单摆摆长与周期关系”的实验中,某同学的主要操作步骤如下: 如图所示,倾角为α的斜面上有一个质量为m的物块,在与斜面成β角斜向上的外力F作用下处于静止状态.已知物块和斜面的动摩擦因数μ<tanα,假设物块与斜面间的最大静摩擦力等于滑动摩擦力.求F的大小范围.
如图所示,倾角为α的斜面上有一个质量为m的物块,在与斜面成β角斜向上的外力F作用下处于静止状态.已知物块和斜面的动摩擦因数μ<tanα,假设物块与斜面间的最大静摩擦力等于滑动摩擦力.求F的大小范围.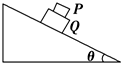 如图所示,质量分别为m和M的两物体P和Q叠放在倾角为θ的斜面上,P、Q之间的动摩擦因数为μ1,Q与斜面间的动摩擦因数为μ2.当它们从静止开始沿斜面下滑时,两物体始终保持相对静止,则
如图所示,质量分别为m和M的两物体P和Q叠放在倾角为θ的斜面上,P、Q之间的动摩擦因数为μ1,Q与斜面间的动摩擦因数为μ2.当它们从静止开始沿斜面下滑时,两物体始终保持相对静止,则