题目内容
19. 在竖直墙壁间有质量为m、倾角为30°的直角楔形木块和质量为2m的光滑圆球,两者能够一起以加速度a匀加速竖直下滑,已知a<g (g为重力加速度).则木块与左侧墙壁之间的动摩擦因数为( )
在竖直墙壁间有质量为m、倾角为30°的直角楔形木块和质量为2m的光滑圆球,两者能够一起以加速度a匀加速竖直下滑,已知a<g (g为重力加速度).则木块与左侧墙壁之间的动摩擦因数为( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
分析 隔离光滑均匀圆球Q,对Q受力分析,根据平衡条件列式求解FN,对两球组成的整体进行受力分析,根据平衡条件列式求解即可.
解答 解:光滑圆球B受力如图所示: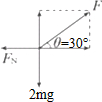
由牛顿第二定律得:FN=Fcosθ,
2mg-Fsinθ=2ma,
对A、B系统,由牛顿第二定律得:
3mg-μFN=3ma,
联立解得:μ=$\frac{\sqrt{3}}{2}$;
故选:A.
点评 解决本题的关键能够正确地受力分析,运用牛顿第二定律进行求解,掌握整体法和隔离法的运用.

练习册系列答案
相关题目
9.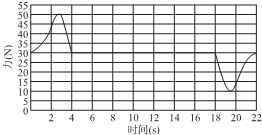 在电梯中,把一重物置于水平台秤上,台秤与力的传感器相连,电梯从静止开始一直上升,最后停止运动:传感器的屏幕上显示出其所受的压力与时间的关系(FN一t)图象,如图所示,则下列说法中正确的是( )
在电梯中,把一重物置于水平台秤上,台秤与力的传感器相连,电梯从静止开始一直上升,最后停止运动:传感器的屏幕上显示出其所受的压力与时间的关系(FN一t)图象,如图所示,则下列说法中正确的是( )
 在电梯中,把一重物置于水平台秤上,台秤与力的传感器相连,电梯从静止开始一直上升,最后停止运动:传感器的屏幕上显示出其所受的压力与时间的关系(FN一t)图象,如图所示,则下列说法中正确的是( )
在电梯中,把一重物置于水平台秤上,台秤与力的传感器相连,电梯从静止开始一直上升,最后停止运动:传感器的屏幕上显示出其所受的压力与时间的关系(FN一t)图象,如图所示,则下列说法中正确的是( )| A. | 0~4s电梯中的物体处于超重状态 | |
| B. | 18~22s内,电梯中的物体处于先超重再失重状态 | |
| C. | 从图中可以求出物体的重力 | |
| D. | 从图中可以找出电梯上升时最大加速度 |
4.下列说法正确的是( )
| A. | 元电荷是指电子或质子本身 | |
| B. | 元电荷的值通常取e=1.60×10-19C | |
| C. | 足够小的电荷就是点电荷 | |
| D. | 点电荷是一种理想模型,实际中并不存在 |
11.某一做直线运动的质点的位移随时间变化的关系式为x=2t2+6t,x与t的单位分别是m和s,则质点的初速度和加速度分别是( )
| A. | 2m/s 12m/s2 | B. | 6m/s 2m/s2 | C. | 6m/s 4m/s2 | D. | 12m/s 4m/s2 |
 某探究学习小组的同学欲以右图装置中的滑块为对象验证“动能定理”,他们在实验室组装了一套如图所示的装置,另外他们还找到了打点计时器所用的学生电源、导线、复写纸、纸带、小木块、细沙、垫块.当滑块连接上纸带,用细线通过滑轮挂上空的小沙桶时,释放小桶,滑块处于静止状态.若你是小组中的一位成员,要完成该项实验,则:
某探究学习小组的同学欲以右图装置中的滑块为对象验证“动能定理”,他们在实验室组装了一套如图所示的装置,另外他们还找到了打点计时器所用的学生电源、导线、复写纸、纸带、小木块、细沙、垫块.当滑块连接上纸带,用细线通过滑轮挂上空的小沙桶时,释放小桶,滑块处于静止状态.若你是小组中的一位成员,要完成该项实验,则: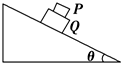 如图所示,质量分别为m和M的两物体P和Q叠放在倾角为θ的斜面上,P、Q之间的动摩擦因数为μ1,Q与斜面间的动摩擦因数为μ2.当它们从静止开始沿斜面下滑时,两物体始终保持相对静止,则
如图所示,质量分别为m和M的两物体P和Q叠放在倾角为θ的斜面上,P、Q之间的动摩擦因数为μ1,Q与斜面间的动摩擦因数为μ2.当它们从静止开始沿斜面下滑时,两物体始终保持相对静止,则



