Question

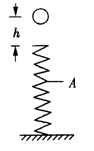
【题目】如图所示，在直角坐标系x0y平面的一、四个象限内各有一个边长为L的正方向区域，二三像限区域内各有一个高L，宽2L的匀强磁场，其中在第二象限内有垂直坐标平面向外的匀强磁场，第一、三、四象限内有垂直坐标平面向内的匀强磁场，各磁场的磁感应强度大小均相等，第一象限的x<L，L<y<2L的区域内，有沿y轴正方向的匀强电场。现有一质量为四电荷量为q的带负电粒子从坐标(L，3L/2)处以初速度沿x轴负方向射入电场，射出电场时通过坐标(0，L)点，不计粒子重力。

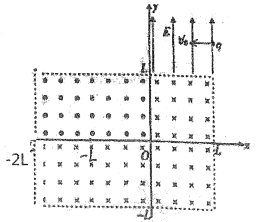
(1)求电场强度大小E；

(2)为使粒子进入磁场后途经坐标原点0到达坐标(-L，0)点，求匀强磁场的磁感应强度大小B；

(3)求第(2)问中粒子从进入磁场到坐标(-L，0)点所用的时间。

Answer 1

【答案】(1)

(2)为使粒子进入磁场后途经坐标原点0到达坐标(-L，0)点，求匀强磁场的磁感应强度大小，n=1、2、3....或，n=1、2、3....

(3) 粒子从进入磁场到坐标(-L，0)点所用的时间为或

【解析】本题考查带电粒子在组合场中的运动，需画出粒子在磁场中的可能轨迹再结合物理公式求解。

(1)带电粒子在电场中做类平抛运动有： ， ，

联立解得：

(2)粒子进入磁场时，速度方向与y 轴负方向夹角的正切值=l

速度大小

设x为每次偏转圆弧对应的弦长，根据运动的对称性，粒子能到达(一L，0 )点，应满足L=2nx，其中n=1、2、3......粒子轨迹如图甲所示，偏转圆弧对应的圆心角为；当满足L=(2n+1)x时，粒子轨迹如图乙所示。

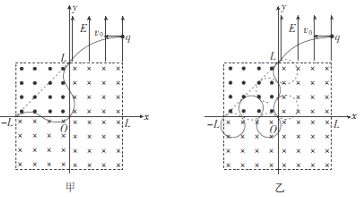
若轨迹如图甲设圆弧的半径为R，圆弧对应的圆心角为.则有x=R，此时满足L=2nx

联立可得：

由牛顿第二定律，洛伦兹力提供向心力，则有：

得： ，n=1、2、3....

轨迹如图乙设圆弧的半径为R，圆弧对应的圆心角为.则有，此时满足

联立可得：

由牛顿第二定律，洛伦兹力提供向心力，则有：

得： ，n=1、2、3....

所以为使粒子进入磁场后途经坐标原点0到达坐标(-L，0)点，求匀强磁场的磁感应强度大小，n=1、2、3....或，n=1、2、3....

(3) 若轨迹如图甲，粒子从进人磁场到从坐标(一L，0)点射出磁场过程中，圆心角的总和θ=2n××2=2nπ，则

若轨迹如图乙，粒子从进人磁场到从坐标(一L，0)点射出磁场过程中，圆心角的总和θ=(2n+1)×2π=(4n+2)π，则

粒子从进入磁场到坐标(-L，0)点所用的时间为或