题目内容
如图所示，长度为L=1.0m的绳，系一小球在竖直面内做圆周运动，小球的质量为M=5kg，小球半径不计，小球在通过最低点时的速度大小为v=20m/s，
求：小球在最低点所受绳的拉力．
解：设小球在最低点所受绳的拉力为F．
由牛顿第二定律得 F-Mg=M
代入解得 F=M（g+）=2050N
答：小球在最低点所受绳的拉力为2050N．
分析：小球在通过最低点时，由重力和绳的拉力提供向心力，由牛顿第二定律求解小球在最低点所受绳的拉力．
点评：本题是圆周运动动力学问题，关键是分析物体的受力情况，确定向心力的来源．
由牛顿第二定律得 F-Mg=M
代入解得 F=M（g+
）=2050N答：小球在最低点所受绳的拉力为2050N．
分析：小球在通过最低点时，由重力和绳的拉力提供向心力，由牛顿第二定律求解小球在最低点所受绳的拉力．
点评：本题是圆周运动动力学问题，关键是分析物体的受力情况，确定向心力的来源．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
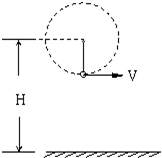（选做B）如图所示，长度为L=1.0m的绳，拴着一质量m=1kg的小球在竖直面内做圆周运动，小球半径不计，已知绳子能够承受的最大张力为74N，圆心离地面高度H=6m，运动过程中绳子始终处于绷紧状态求：
如图所示，长度为L=1.0m的绳，系一小球在竖直面内做圆周运动，小球的质量为M=5kg，小球半径不计，小球在通过最低点的速度大小为v=20m/s，试求：
（2008?崇文区一模）如图所示，长度为L=0.2m、电阻r=0.3Ω、质量m=0.1kg的金属棒CD，垂直跨搁在位于水平面上的两条平行光滑的金属导轨上，导轨间距离也为L，棒与导轨间接触良好，导轨电阻不计．导轨左端接有R=0.5Ω的电阻，垂直导轨平面的匀强磁场向下穿过导轨平面，磁感强度B=4T．现以水平向右的恒定外力F使金属棒右移，当金属棒以v=2m/s的速度在导轨平面上匀速滑动时，求：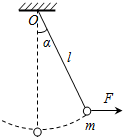
（2011?北京）如图所示，长度为l的轻绳上端固定在O点，下端系一质量为m的小球（小球的大小可以忽略）．
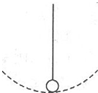如图所示，长度为L=1.0m的绳，系一小球在竖直面内做圆周运动，小球的质量为M=5kg，小球半径不计，小球在通过最低点时的速度大小为v=20m/s，