题目内容
 (2011?北京)如图所示,长度为l的轻绳上端固定在O点,下端系一质量为m的小球(小球的大小可以忽略).
(2011?北京)如图所示,长度为l的轻绳上端固定在O点,下端系一质量为m的小球(小球的大小可以忽略).(1)在水平拉力F的作用下,轻绳与竖直方向的夹角为α,小球保持静止.画出此时小球的受力图,并求力F的大小;
(2)由图示位置无初速释放小球,求当小球通过最低点时的速度大小及轻绳对小球的拉力.不计空气阻力.
分析:(1)为了求出F的大小,我们首先做出小球此时的受力示意图,根据共点力平衡条件求出F;
(2)小球向下摆动的时候只有重力做功,所以用机械能守恒定律可以求出最低点的速度,
在最低点根据合力充当向心力,由牛顿第二定律列出向心力方程,可以求出绳子对小球的拉力.
(2)小球向下摆动的时候只有重力做功,所以用机械能守恒定律可以求出最低点的速度,
在最低点根据合力充当向心力,由牛顿第二定律列出向心力方程,可以求出绳子对小球的拉力.
解答:解:(1)受力图如图所示
根据平衡条件小球受到的拉力大小F=mgtanα

(2)运动中只有重力做功,系统机械能守恒mgl(1-cosα)=
mv2
则通过最低点时,小球的速度大小v=
根据牛顿第二定律 T′-mg=m
解得轻绳对小球的拉力T′=mg+m
=mg(3-2cosα),方向竖直向上
答:(1)小球受到的拉力为mgtanα
(2)通过最低点时,小球的速度大为v=
轻绳对小球的拉力为mg(3-2cosα),方向竖直向上.
根据平衡条件小球受到的拉力大小F=mgtanα

(2)运动中只有重力做功,系统机械能守恒mgl(1-cosα)=
| 1 |
| 2 |
则通过最低点时,小球的速度大小v=
| 2gl(1-cosα) |
根据牛顿第二定律 T′-mg=m
| v2 |
| l |
解得轻绳对小球的拉力T′=mg+m
| v2 |
| l |
答:(1)小球受到的拉力为mgtanα
(2)通过最低点时,小球的速度大为v=
| 2gl(1-cosα) |
轻绳对小球的拉力为mg(3-2cosα),方向竖直向上.
点评:本题的关键是首先根据受力分析做出力的示意图;
根据机械能守恒求出最低点的速度,正确列出向心力方程.是一道综合性较好的中档题目.
根据机械能守恒求出最低点的速度,正确列出向心力方程.是一道综合性较好的中档题目.

练习册系列答案
相关题目
 (2011?北京)“蹦极”就是跳跃者把一端固定的长弹性绳绑在踝关节等处,从几十米高处跳下的一种极限运动.某人做蹦极运动,所受绳子拉力F的大小随时间t变化的情况如图所示.将蹦极过程近似为在竖直方向的运动,重力加速度为g.据图可知,此人在蹦极过程中最大加速度约为( )
(2011?北京)“蹦极”就是跳跃者把一端固定的长弹性绳绑在踝关节等处,从几十米高处跳下的一种极限运动.某人做蹦极运动,所受绳子拉力F的大小随时间t变化的情况如图所示.将蹦极过程近似为在竖直方向的运动,重力加速度为g.据图可知,此人在蹦极过程中最大加速度约为( ) (2011?北京)利用电场和磁场,可以将比荷不同的离子分开,这种方法在化学分析和原子核技术等领域有重要的应用.如图所示的矩形区域ACDG(AC边足够长)中存在垂直于纸面的匀强磁场,A处有一狭缝.离子源产生的离子,经静电场加速后穿过狭缝沿垂直于GA边且垂直于磁场的方向射入磁场,运动到GA边,被相应的收集器收集.整个装置内部为真空.已知被加速的两种正离子的质量分别是m1和m2(m1>m2),电荷量均为q.加速电场的电势差为U,离子进入电场时的初速度可以忽略.不计重力,也不考虑离子间的相互作用.
(2011?北京)利用电场和磁场,可以将比荷不同的离子分开,这种方法在化学分析和原子核技术等领域有重要的应用.如图所示的矩形区域ACDG(AC边足够长)中存在垂直于纸面的匀强磁场,A处有一狭缝.离子源产生的离子,经静电场加速后穿过狭缝沿垂直于GA边且垂直于磁场的方向射入磁场,运动到GA边,被相应的收集器收集.整个装置内部为真空.已知被加速的两种正离子的质量分别是m1和m2(m1>m2),电荷量均为q.加速电场的电势差为U,离子进入电场时的初速度可以忽略.不计重力,也不考虑离子间的相互作用.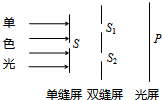 (2011?北京)如图所示的双缝干涉实验,用绿光照射单缝S时,在光屏P上观察到干涉条纹.要得到相邻条纹间距更大的干涉图样,可以( )
(2011?北京)如图所示的双缝干涉实验,用绿光照射单缝S时,在光屏P上观察到干涉条纹.要得到相邻条纹间距更大的干涉图样,可以( )