题目内容
在一只静止的小船上练习射击,船、人连同枪(不包括子弹)及靶的总质量为M,枪内装有n颗子弹,每颗质量为m,枪口到靶的距离为l,子弹射出枪口时相对于地面的速度为v,在发射后一颗子弹时,前一颗子弹已陷入靶中,则在发射完n颗子弹后,小船后退的距离为多少?

【错解分析】错解: 设第一颗子弹射出后船的后退速度为v′,后退距离为S1,子弹从枪口到靶所用的时间为:
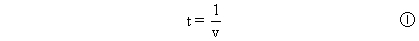
对这颗子弹和其他物体构成的系统列动量守恒方程:
mv = [M+(n-1)m]v′ ②
在时间t内船的后退距离
s1= v′t ③
子弹全部射出后船的后退距离
s = ns1④
联立①②③④解得:
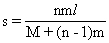

【正确解答】 设子弹射出后船的后退速度为v′,后退距离为s1=v′t,如图5-5所示,由几何关系可知
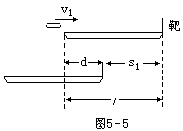
l= d+s1即l=v·t + v′t ⑤
联立②③④⑤解得:

【小结】 对本题物理过程分析的关键,是要弄清子弹射向靶的过程中,子弹与船运动的关系,而这一关系如果能用图5-5所示的几何图形加以描述,则很容易找出子弹与船间的相对运动关系。可见利用运动的过程草图,帮助我们分析类似较为复杂的运动关系问题,是大有益处的。
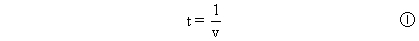
对这颗子弹和其他物体构成的系统列动量守恒方程:
mv = [M+(n-1)m]v′ ②
在时间t内船的后退距离
s1= v′t ③
子弹全部射出后船的后退距离
s = ns1④
联立①②③④解得:
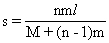

【正确解答】 设子弹射出后船的后退速度为v′,后退距离为s1=v′t,如图5-5所示,由几何关系可知

l= d+s1即l=v·t + v′t ⑤
联立②③④⑤解得:

【小结】 对本题物理过程分析的关键,是要弄清子弹射向靶的过程中,子弹与船运动的关系,而这一关系如果能用图5-5所示的几何图形加以描述,则很容易找出子弹与船间的相对运动关系。可见利用运动的过程草图,帮助我们分析类似较为复杂的运动关系问题,是大有益处的。

练习册系列答案
相关题目

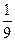 ,那么小球B的速度可能是( )
,那么小球B的速度可能是( )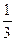 v0
v0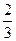 v0
v0 v0
v0 v0
v0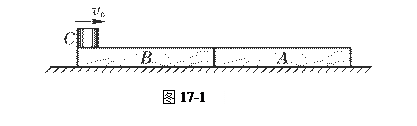



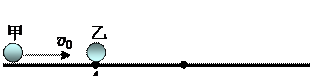
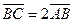 。已知小球间的碰撞及小球与墙壁之间的碰撞均无机械能损失,求甲、乙两球的质量之比
。已知小球间的碰撞及小球与墙壁之间的碰撞均无机械能损失,求甲、乙两球的质量之比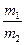 。
。