题目内容
5. 如图所示,半径为R=2m的光滑绝缘半圆轨道ABC与倾角θ=37°的粗糙绝缘斜面轨道DC相切于C,圆轨道的直径AC与斜面垂直,虚线框为电场区域,左边界过C点,初始内部无电场.质量为m=2kg的带正电q的小球以初速度v0=4m/s相切于A点进入半圆轨道内存,之后经半圆轨道沿斜面刚好滑到与A点等高的D处,此时虚线框内出现E=$\frac{3mg}{4q}$水平向左的匀强电场.已知当地的重力加速度为g=10m/s2,sin37°=0.6,cos37°=0.8
如图所示,半径为R=2m的光滑绝缘半圆轨道ABC与倾角θ=37°的粗糙绝缘斜面轨道DC相切于C,圆轨道的直径AC与斜面垂直,虚线框为电场区域,左边界过C点,初始内部无电场.质量为m=2kg的带正电q的小球以初速度v0=4m/s相切于A点进入半圆轨道内存,之后经半圆轨道沿斜面刚好滑到与A点等高的D处,此时虚线框内出现E=$\frac{3mg}{4q}$水平向左的匀强电场.已知当地的重力加速度为g=10m/s2,sin37°=0.6,cos37°=0.8(1)小球从A到D的整个过程中摩擦力做的功W;
(2)小球到达半圆轨道最低点B时,对轨道的压力大小;
(3)在D点应给小球多大初动能EK,才能使小球沿轨道向下运动恰好返回A点?
分析 (1)小球沿斜面上滑过程中,根据动能定理求解W;
(2)从抛出点到B的过程中,根据动能定理列式,在B点,根据向心力公式列式,联立方程即可求解;
(3)刚好能到达A点,由重力与电场力的合力提供向心力,根据向心力公式列式,由D到A的过程中,根据动能定理列式,联立方程即可求解.
解答 解:(1)小球沿斜面上滑过程中,根据动能定理得:
${W}_{f}=0-\frac{1}{2}m{{v}_{0}}^{2}=-16J$
(2)设小球达到B点的速度为v,则从抛出点到B的过程中,根据动能定理得:
$mgR(1+cos37°)=\frac{1}{2}m{v}^{2}-\frac{1}{2}m{{v}_{0}}^{2}$
在B点,根据向心力公式得:
${F}_{N}-mg=m\frac{{v}^{2}}{R}$
解得:FN=108N
由牛顿第三定律可知,小球在B点对轨道的压力大小为108N,方向向下,
(3)刚好能到达A点,由重力与电场力的合力提供向心力,则有:
F=$\frac{5}{4}mg=m\frac{{{v}_{A}}^{2}}{R}$
解得:${v}_{A}=\sqrt{\frac{5}{4}gR}$
由D到A的过程中,根据动能定理得:
$W-2EqEsin37°=\frac{1}{2}m{{v}_{A}}^{2}-{E}_{K}$
解得:EK=77J
答:(1)小球从A到D的整个过程中摩擦力做的功W为-16J;
(2)小球到达半圆轨道最低点B时,对轨道的压力大小为108N;
(3)在D点应给小球77J的初动能EK,才能使小球沿轨道向下运动恰好返回A点.
点评 本题主要考查了动能定理以及向心力公式的直接应用,解题时要选择合适的研究对象和研究过程列式,注意刚好能到达A点,则在A点由重力与电场力的合力提供向心力,难度适中.

| A. | 在照相机镜头前加装偏振滤光片拍摄日落时的景物,可使景象更清晰 | |
| B. | 太阳光通过三棱镜形成彩色光谱,这是光的干涉的结果 | |
| C. | 用光导纤维束传送图象信息,这是光的衍射的应用 | |
| D. | 透过平行于日光灯的窄缝观察正常发光的日光灯时能看到彩色条纹,这是光的色散现象 |
 两块平行金属板M、N水平放置,带电情况如图所示并保持电量不变,其内部空间有两个静止悬浮着的小带电液滴A和B,则( )
两块平行金属板M、N水平放置,带电情况如图所示并保持电量不变,其内部空间有两个静止悬浮着的小带电液滴A和B,则( )| A. | 带电液滴A和B带负电 | |
| B. | 使两板左、右错开一些可使液滴向下做加速运动 | |
| C. | 使两板靠近一些仍保持静止 | |
| D. | 使A和B粘合在一起会向下运动 |
 带有滑轮的滑块穿过水平的杆,小球A、B分别穿过竖直的杆并用轻绳跨过定滑轮连接在一起,用手分别托住 A、B,此时线和竖直夹角分别为30°和60°度,如图所示,调整两球位置,使其移开双手后A、B能处于静止状态,则A、B两球的质量比(不计一切摩擦力)( )
带有滑轮的滑块穿过水平的杆,小球A、B分别穿过竖直的杆并用轻绳跨过定滑轮连接在一起,用手分别托住 A、B,此时线和竖直夹角分别为30°和60°度,如图所示,调整两球位置,使其移开双手后A、B能处于静止状态,则A、B两球的质量比(不计一切摩擦力)( )| A. | 1:$\sqrt{3}$ | B. | 1:1 | C. | $\sqrt{3}$:1 | D. | 无法判断 |
| A. | “北斗一号”系统中的三颗卫星质量必须相同,否则它们不能定位在同一轨道上 | |
| B. | GPS的卫星较“北斗一号”的卫星周期更长 | |
| C. | GPS的卫星较“北斗一号”的卫星有更大的加速度 | |
| D. | GPS的卫星较“北斗一号”的卫星有较小的运行速度 |
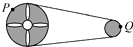 如图所示是自行车的轮盘与车轴上的飞轮之间的链条传动装置.P是轮盘的一个齿,Q是飞轮上的一个齿.下列说法中正确的是( )
如图所示是自行车的轮盘与车轴上的飞轮之间的链条传动装置.P是轮盘的一个齿,Q是飞轮上的一个齿.下列说法中正确的是( )| A. | P、Q两点角速度大小相等 | B. | P点线速度小于Q点线速度 | ||
| C. | P点线速度大于Q点线速度 | D. | P点向心加速度小于Q点向心加速度 |

 交流发电机的发电原理是矩形线圈在匀强磁场中绕垂直于磁场的轴OO′匀速转动.一小型发电机的线圈共220匝,线圈面积S=0.05m2,线圈转动的频率为50Hz,线圈内阻不计,磁场的磁感应强度B=$\frac{\sqrt{2}}{π}$ T.为用此发电机所发出交变电流带动两个标有“220V,11kW”的电机正常工作,需在发电机的输出端a、b与电机之间接一个理想变压器,电路如图所示,求:
交流发电机的发电原理是矩形线圈在匀强磁场中绕垂直于磁场的轴OO′匀速转动.一小型发电机的线圈共220匝,线圈面积S=0.05m2,线圈转动的频率为50Hz,线圈内阻不计,磁场的磁感应强度B=$\frac{\sqrt{2}}{π}$ T.为用此发电机所发出交变电流带动两个标有“220V,11kW”的电机正常工作,需在发电机的输出端a、b与电机之间接一个理想变压器,电路如图所示,求: