题目内容
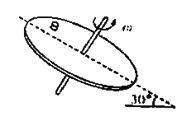
【题目】如图所示,在某行星表面上有一倾斜的匀质圆盘,盘面与水平面的夹角为30°,圆盘绕垂直于盘面的固定对称轴以恒定的角速度转动,盘面上离转轴距离L处有一小物体与圆盘保持相对静止,当圆盘的角速度为![]() 时,小物块刚要滑动。物体与盘面间的动摩擦因数为
时,小物块刚要滑动。物体与盘面间的动摩擦因数为![]() (设最大静摩擦力等于滑动摩擦力),该星球的半径为R,引力常量为G,下列说法正确的是( )
(设最大静摩擦力等于滑动摩擦力),该星球的半径为R,引力常量为G,下列说法正确的是( )
A.这个行星的质量M=![]()
B.这个行星的同步卫星的周期是![]()
C.这个行星的第一宇宙速度![]()
D.离行星表面距离为R的地方的重力加速度为![]()
【答案】D
【解析】
A.当物体运动到圆盘最低点时,此时所受静摩擦延半径方向向上达到最大,此时对应的角速度为最大值,则由牛顿第二定律有
![]()
解得
![]()
绕行星表面做匀速圆周运动的物体,万有引力提供向心力,则有
![]()
解得
![]()
故A错误;
B.由于不知道同步卫星高度,无法求得同步卫星周期,故B错误;
C.当万有引力提供向心力,轨道等于行星半径时,可求得该行星第一宇宙速度为
![]()
故C错误;
D.离星球表面距离为R的地方万有引力为
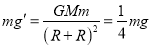
解得
![]()
故D正确。
故选D。

练习册系列答案
相关题目