题目内容
(10分)如图所示,一质量为M的滑块静止在光滑的水平面上,其左侧是一光滑的四分之一圆弧,圆弧半径为R=1m,一质量为m的小球以速度V0向右运动冲上滑块,已知M=4m,g取10 m/s2,若小球刚好没跃出圆弧的上端,求:
①小球的初速度V0是多少?
②滑块获得的最大速度是多少?
V0=5m/s V2=2m/S
解析试题分析:①由题意,当小球上升到滑块上端时,小球与滑块水平方向速度相同,设为V1,
在水平方向上,由动量守恒
mV0=(m+M)V1 (2分)
由机械能守恒定律 (2分)
(2分)
解得V0=5m/s (1分)
②当小球离开滑块后滑块速度最大, 设其最大速度为V2,小球的速度为V3
由动量守恒
mV0=MV2+mV3 (2分)
由机械能守恒定律 (2分)
(2分)
解得 V2=2m/S (1分)
考点:本题考查动量守恒定律、机械能守恒定律。

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
如右图所示,在倾角θ=30°的光滑固定斜面上,放有两个质量分别为1 kg和2 kg的可视为质点的小球A和B,两球之间用一根长L=0.2 m的轻杆相连,小球B距水平面的高度h=0.1 m.两球从静止开始下滑到光滑地面上,不计球与地面碰撞时的机械能损失,g取10 m/s2.则下列说法中正确的是( )
| A.下滑的整个过程中A球机械能守恒 |
| B.下滑的整个过程中两球组成的系统机械能守恒 |
| C.两球在光滑水平面上运动时的速度大小为2 m/s |
| D.下滑的整个过程中B球机械能的增加量为 J |
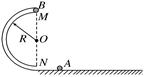
 (q>0)的小球自A点由静止开始下滑,小球沿轨道到达最高点C时恰好对轨道没有压力,小球经过B点时无机械能损失,已知A离地面高度 H=2.5R,AO间距离L=3R,重力加速度为g,静电力常量为k,求:
(q>0)的小球自A点由静止开始下滑,小球沿轨道到达最高点C时恰好对轨道没有压力,小球经过B点时无机械能损失,已知A离地面高度 H=2.5R,AO间距离L=3R,重力加速度为g,静电力常量为k,求: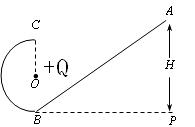

 ,为使A、B达到共同速度前A不滑离木板,木板至少多长?
,为使A、B达到共同速度前A不滑离木板,木板至少多长?