题目内容
19. 如图所示,一带电量为q=2×10-9c,质量为m=2×10-16kg的粒子,在直线上一点O沿30°角方向进入磁感应强度B=0.2T的匀强磁场中(磁场在直线上方的区域足够大),已知OP的距离为0.5m,求:
如图所示,一带电量为q=2×10-9c,质量为m=2×10-16kg的粒子,在直线上一点O沿30°角方向进入磁感应强度B=0.2T的匀强磁场中(磁场在直线上方的区域足够大),已知OP的距离为0.5m,求:(1)粒子的运动速率v为多大;
(2)粒子在磁场中运动的时间;
(3)若仅使题中的磁感应强度反向,则前后两次带电粒子在磁场中运动的时间之比为多少?
分析 (1)求出粒子在磁场中转过的圆心角,结合几何关系得到轨道半径,根据牛顿第二定律列式求解出粒子的运动速率;
(2)根据t=$\frac{θR}{v}$求解运动时间;
(3)先画出轨迹,求解出临界角,根据t=$\frac{θ}{2π}T$求解时间,得到比值.
解答 解:(1)粒子运动轨迹如图所示: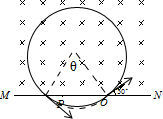
由几何知识可知,粒子在磁场中转过的圆心角:
α=360°-θ=360°-2×30°=300°,
由几何关系可得:R=0.5m
由 $qvB=m\frac{{v}^{2}}{r}$可得:v=$\frac{qBR}{m}$
代入得:v=106m/s
(2)运动时间:t1=$\frac{θR}{v}=\frac{\frac{π}{3}×0.5}{1{0}^{6}}$=$\frac{5}{6}π×1{0}^{-6}s$
(3)当磁场方向反向时,带电粒子在磁场中运动轨迹所对应的圆心角:$θ=\frac{π}{3}$,
则${t}_{2}=\frac{θR}{v}$=$\frac{\frac{π}{6}×0.5}{1{0}^{6}}$=$\frac{5}{12}π×1{0}^{-6}s$,
故$\frac{{t}_{1}}{{t}_{2}}$=$\frac{5}{1}$
答:(1)粒子的运动速率v为为106m/s;
(2)粒子在磁场中运动的时间为$\frac{5}{6}π×1{0}^{-6}s$;
(3)若仅使题中的磁感应强度反向,则前后两次带电粒子在磁场中运动的时间之比为5:1.
点评 本题考查了粒子在磁场中的运动,粒子在磁场中做匀速圆周运动,分析清楚粒子运动过程,应用周期公式、牛顿第二定律即可正确解题,解题时注意数学知识的应用.

练习册系列答案
相关题目
7. xOy平面内以O为圆心的圆形区域内有一方向垂直xOy平面的匀强磁场.一个质量为m、电荷量为q的带电粒子由原点O开始运动,初速度为v,方向沿x轴正方向.后来,粒子经过y轴上的P点,如图所示.不计重力的影响,粒子经过P点时的速度方向可能是( )
xOy平面内以O为圆心的圆形区域内有一方向垂直xOy平面的匀强磁场.一个质量为m、电荷量为q的带电粒子由原点O开始运动,初速度为v,方向沿x轴正方向.后来,粒子经过y轴上的P点,如图所示.不计重力的影响,粒子经过P点时的速度方向可能是( )
 xOy平面内以O为圆心的圆形区域内有一方向垂直xOy平面的匀强磁场.一个质量为m、电荷量为q的带电粒子由原点O开始运动,初速度为v,方向沿x轴正方向.后来,粒子经过y轴上的P点,如图所示.不计重力的影响,粒子经过P点时的速度方向可能是( )
xOy平面内以O为圆心的圆形区域内有一方向垂直xOy平面的匀强磁场.一个质量为m、电荷量为q的带电粒子由原点O开始运动,初速度为v,方向沿x轴正方向.后来,粒子经过y轴上的P点,如图所示.不计重力的影响,粒子经过P点时的速度方向可能是( )| A. | 箭头a | B. | 箭头b | C. | 箭头c | D. | 箭头d |
14.已知月球半径为R,飞船在距月球表面高度为R的圆轨道上飞行,周期为T,万有引力常量为G,下列说法正确的是( )
| A. | 月球质量为$\frac{32{π}^{2}{R}^{3}}{G{T}^{2}}$ | B. | 月球表面重力加速度为$\frac{8{π}^{2}}{{T}^{2}}$R | ||
| C. | 月球密度为$\frac{3π}{G{T}^{2}}$ | D. | 月球第一宇宙速度为$\frac{4πR}{T}$ |
11. 图中是科大著名服务机器人“可佳”.如图所示,现要执行一项任务.给它设定了如下动作程序:机器人在平面内,由点(0,0)出发,沿直线运动到点(3,1),然后又由点(3,1)沿直线运动到点(1,4),然后又由点(1,4)沿直线运动到点(5,5),然后又由点(5,5)沿直线运动到点(2,2),整个过程中机器人所用时间是2$\sqrt{2}$s,则( )
图中是科大著名服务机器人“可佳”.如图所示,现要执行一项任务.给它设定了如下动作程序:机器人在平面内,由点(0,0)出发,沿直线运动到点(3,1),然后又由点(3,1)沿直线运动到点(1,4),然后又由点(1,4)沿直线运动到点(5,5),然后又由点(5,5)沿直线运动到点(2,2),整个过程中机器人所用时间是2$\sqrt{2}$s,则( )
 图中是科大著名服务机器人“可佳”.如图所示,现要执行一项任务.给它设定了如下动作程序:机器人在平面内,由点(0,0)出发,沿直线运动到点(3,1),然后又由点(3,1)沿直线运动到点(1,4),然后又由点(1,4)沿直线运动到点(5,5),然后又由点(5,5)沿直线运动到点(2,2),整个过程中机器人所用时间是2$\sqrt{2}$s,则( )
图中是科大著名服务机器人“可佳”.如图所示,现要执行一项任务.给它设定了如下动作程序:机器人在平面内,由点(0,0)出发,沿直线运动到点(3,1),然后又由点(3,1)沿直线运动到点(1,4),然后又由点(1,4)沿直线运动到点(5,5),然后又由点(5,5)沿直线运动到点(2,2),整个过程中机器人所用时间是2$\sqrt{2}$s,则( )| A. | 机器人的运动轨迹是一条直线 | |
| B. | 机器人有两次通过同一点 | |
| C. | 整个过程中机器人的位移大小为$\sqrt{2}$m | |
| D. | 整个过程中机器人的平均速率为1m/s |
8.质量为m的滑块以一定初速度滑上倾角为θ的固定斜面,同时施加一沿斜面向上的恒力F=mgsinθ,已知滑块与斜面间的动摩擦因数μ=tanθ,取出发点为参考点,在滑块从开始运动到最高点的过程中,下列叙述正确的是( )
| A. | 滑块机械能守恒 | |
| B. | 滑块减少的动能大于克服摩擦产生的内能 | |
| C. | 滑块减少的动能等于克服摩擦产生的内能和增加的势能之和 | |
| D. | 滑块减少的动能大于增加的势能 |
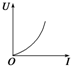
9. 如图所示,直线A为某电源的U-I图线,曲线B为某小灯泡D1的U-I图线的一部分,用该电源和小灯泡D1组成闭合电路时,灯泡D1恰好能正常发光,则下列说法中正确的是( )
如图所示,直线A为某电源的U-I图线,曲线B为某小灯泡D1的U-I图线的一部分,用该电源和小灯泡D1组成闭合电路时,灯泡D1恰好能正常发光,则下列说法中正确的是( )
 如图所示,直线A为某电源的U-I图线,曲线B为某小灯泡D1的U-I图线的一部分,用该电源和小灯泡D1组成闭合电路时,灯泡D1恰好能正常发光,则下列说法中正确的是( )
如图所示,直线A为某电源的U-I图线,曲线B为某小灯泡D1的U-I图线的一部分,用该电源和小灯泡D1组成闭合电路时,灯泡D1恰好能正常发光,则下列说法中正确的是( )| A. | 此电源的电动势为4V | |
| B. | 此电源的内阻为$\frac{2}{3}$Ω | |
| C. | 灯泡D1的额定电压为3V,功率为6W | |
| D. | 把灯泡D1换成一个1Ω的定值电阻,电源的输出功率将变小 |



 如图所示,半径为L1=2m的金属圆环内上、下半圆各有垂直圆环平面的有界匀强磁场,磁感应强度大小均为B1=$\frac{10}{π}$ T.长度也为L1、电阻为R的金属杆ab,一端处于圆环中心,另一端恰好搭接在金属环上,绕着a端沿逆时针方向匀速转动,角速度为ω=$\frac{π}{10}$ rad/s.通过导线将金属杆的a端和金属环连接到图示的电路中(连接a端的导线与圆环不接触,图中的定值电阻R1=R,滑片P位于R2的正中央,R2的总阻值为4R),图中的平行板长度为L2=2m,宽度为d=2m.图示位置为计时起点,在平行板左边缘中央处刚好有一带电粒子以初速度v0=0.5m/s向右运动,并恰好能从平行板的右边缘飞出,之后进入到有界匀强磁场中,其磁感应强度大小为B2,左边界为图中的虚线位置,右侧及上下范围均足够大.(忽略金属杆与圆环的接触电阻、圆环电阻及导线电阻,忽略电容器的充放电时间,忽略带电粒子在磁场中运动时的电磁辐射的影响,不计平行金属板两端的边缘效应及带电粒子的重力和空气阻力)求:
如图所示,半径为L1=2m的金属圆环内上、下半圆各有垂直圆环平面的有界匀强磁场,磁感应强度大小均为B1=$\frac{10}{π}$ T.长度也为L1、电阻为R的金属杆ab,一端处于圆环中心,另一端恰好搭接在金属环上,绕着a端沿逆时针方向匀速转动,角速度为ω=$\frac{π}{10}$ rad/s.通过导线将金属杆的a端和金属环连接到图示的电路中(连接a端的导线与圆环不接触,图中的定值电阻R1=R,滑片P位于R2的正中央,R2的总阻值为4R),图中的平行板长度为L2=2m,宽度为d=2m.图示位置为计时起点,在平行板左边缘中央处刚好有一带电粒子以初速度v0=0.5m/s向右运动,并恰好能从平行板的右边缘飞出,之后进入到有界匀强磁场中,其磁感应强度大小为B2,左边界为图中的虚线位置,右侧及上下范围均足够大.(忽略金属杆与圆环的接触电阻、圆环电阻及导线电阻,忽略电容器的充放电时间,忽略带电粒子在磁场中运动时的电磁辐射的影响,不计平行金属板两端的边缘效应及带电粒子的重力和空气阻力)求: