题目内容
14.已知月球半径为R,飞船在距月球表面高度为R的圆轨道上飞行,周期为T,万有引力常量为G,下列说法正确的是( )| A. | 月球质量为$\frac{32{π}^{2}{R}^{3}}{G{T}^{2}}$ | B. | 月球表面重力加速度为$\frac{8{π}^{2}}{{T}^{2}}$R | ||
| C. | 月球密度为$\frac{3π}{G{T}^{2}}$ | D. | 月球第一宇宙速度为$\frac{4πR}{T}$ |
分析 飞船绕月球飞行做匀速圆周运动,由万有引力提供圆周运动向心力,据此讨论分析即可.
解答 解:飞船在距月球表面高度为R的圆轨道上飞行时的轨道半径r=R+R=2R
A、据万有引力提供圆周运动向心力有:
$G\frac{mM}{{r}^{2}}=mr\frac{4{π}^{2}}{{T}^{2}}$
可得月球的质量M=$\frac{4{π}^{2}{r}^{3}}{G{T}^{2}}=\frac{32{π}^{2}{R}^{3}}{G{T}^{2}}$,故A正确;
B、据月球表面重力与万有引力相等有:$G\frac{mM}{{R}^{2}}=mg$,可得月球表面重力加速度g=$G\frac{M}{{R}^{2}}=\frac{32{π}^{2}R}{{T}^{2}}$,故B错误;
C、根据密度公式可知,月球密度$ρ=\frac{M}{V}=\frac{\frac{32{π}^{2}{R}^{3}}{G{T}^{2}}}{\frac{4}{3}π{R}^{3}}=\frac{24{π}^{2}}{G{T}^{2}}$,故C错误;
D、据万有引力提供圆周运动向心力可得近月圆周运动的速度即第一宇宙速度v=$\sqrt{\frac{GM}{R}}=\sqrt{\frac{32{π}^{2}{R}^{2}}{{T}^{2}}}=4\sqrt{2}\frac{πR}{T}$,故D错误.
故选:A.
点评 掌握万有引力提供圆周运动向心力和在月球表面重力与万有引力相等是解决问题的关键,本题易错点在于对星球半径与飞船轨道半径的确认.

练习册系列答案
相关题目
16.一物体自t=0时开始做直线运动,其速度图线如图所示,下列选项正确的是( ) 

| A. | 在0~6s内,物体经过的路程为40m | |
| B. | 在0~6s内,物体离出发点最远为30m | |
| C. | 在0~4s内,物体的平均速度为7.5m/s | |
| D. | 在4s~6s内,物体一直做匀减速直线运动 |
6.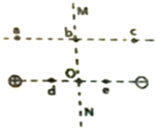 如图所示,在两等量异种点电荷的电场中,O为两电荷连线中点,MN为两电荷连线的中垂线,a、b、c三点所在直线平行于两电荷的连线,且a、c关于MN对称,b点位于MN上,d、e位于两电荷的连线上,且d、e关于MN对称,以下判断正确的是( )
如图所示,在两等量异种点电荷的电场中,O为两电荷连线中点,MN为两电荷连线的中垂线,a、b、c三点所在直线平行于两电荷的连线,且a、c关于MN对称,b点位于MN上,d、e位于两电荷的连线上,且d、e关于MN对称,以下判断正确的是( )
 如图所示,在两等量异种点电荷的电场中,O为两电荷连线中点,MN为两电荷连线的中垂线,a、b、c三点所在直线平行于两电荷的连线,且a、c关于MN对称,b点位于MN上,d、e位于两电荷的连线上,且d、e关于MN对称,以下判断正确的是( )
如图所示,在两等量异种点电荷的电场中,O为两电荷连线中点,MN为两电荷连线的中垂线,a、b、c三点所在直线平行于两电荷的连线,且a、c关于MN对称,b点位于MN上,d、e位于两电荷的连线上,且d、e关于MN对称,以下判断正确的是( )| A. | b点场强大于d点场强 | B. | a点场强与c点场强相同 | ||
| C. | d点场强与e点场强相同 | D. | O点场强为零 |
3.地球自转一天的时间为T,地球表面的重力加速度为g,地球的半径为R.一卫星Q位于赤道上空,赤道上一城市A的人每三天可以看到Q四次掠过上空,则Q卫星的轨道半径表达式为( )
| A. | r3=($\frac{3T}{14π}$)2R2g | B. | r3=($\frac{3T}{8π}$)2R2g | C. | r3=($\frac{T}{2π}$)2R2g | D. | r3=($\frac{2T}{3π}$)2R2g |
4. 在如图(a)所示的电路中,R1为定值电阻,R2为滑动变阻器,闭合电键S,将滑动变阻器的滑动触头P从最右端滑到最左端,两个电压表的示数随电路中电流变化的完整过程图线如图(b)所示,则( )
在如图(a)所示的电路中,R1为定值电阻,R2为滑动变阻器,闭合电键S,将滑动变阻器的滑动触头P从最右端滑到最左端,两个电压表的示数随电路中电流变化的完整过程图线如图(b)所示,则( )
 在如图(a)所示的电路中,R1为定值电阻,R2为滑动变阻器,闭合电键S,将滑动变阻器的滑动触头P从最右端滑到最左端,两个电压表的示数随电路中电流变化的完整过程图线如图(b)所示,则( )
在如图(a)所示的电路中,R1为定值电阻,R2为滑动变阻器,闭合电键S,将滑动变阻器的滑动触头P从最右端滑到最左端,两个电压表的示数随电路中电流变化的完整过程图线如图(b)所示,则( )| A. | 电源的电动势为6V | B. | 电源内电阻的阻值为10Ω | ||
| C. | 滑动变阻器的最大阻值为20Ω | D. | 电源的最大输出功率为0.8W |
 如图所示,轻杆一端A固定在水平地面上,另一端B装有一小滑轮,一轻绳的一端C固定于地面上,另一端D跨过滑轮后施加100N的拉力,∠CBA=30°,∠ABD=76°,求滑轮受到绳子的作用力大小及方向.
如图所示,轻杆一端A固定在水平地面上,另一端B装有一小滑轮,一轻绳的一端C固定于地面上,另一端D跨过滑轮后施加100N的拉力,∠CBA=30°,∠ABD=76°,求滑轮受到绳子的作用力大小及方向. 如图为一个利用电场、磁场对电荷运动控制的模型图.在区域I中的P1、P2分别为加速电场的正负两极板,P2中央有一孔,两极板竖直平行正对放置,开始加有大小为U的电压;在区域Ⅱ中有一以l及l′为边界的竖直向下的匀强电场;在区域Ⅲ中有一以l′为左边界垂直于纸面的匀强磁场.现有一带正电的粒子(重力不计)质量为m,电量为q,从极板P1由静止开始沿中轴线OO′方向进入区域Ⅱ,从边界l′的P点离开区域Ⅱ,此时速度与水平方向夹角α=30°.若将P1、P2两极板所加电压改为U′,其它条件不变,粒子则从边界l′的Q点离开区域Ⅱ,此时速度与水平方向夹角β=60°.已知PQ两点的距离为d.
如图为一个利用电场、磁场对电荷运动控制的模型图.在区域I中的P1、P2分别为加速电场的正负两极板,P2中央有一孔,两极板竖直平行正对放置,开始加有大小为U的电压;在区域Ⅱ中有一以l及l′为边界的竖直向下的匀强电场;在区域Ⅲ中有一以l′为左边界垂直于纸面的匀强磁场.现有一带正电的粒子(重力不计)质量为m,电量为q,从极板P1由静止开始沿中轴线OO′方向进入区域Ⅱ,从边界l′的P点离开区域Ⅱ,此时速度与水平方向夹角α=30°.若将P1、P2两极板所加电压改为U′,其它条件不变,粒子则从边界l′的Q点离开区域Ⅱ,此时速度与水平方向夹角β=60°.已知PQ两点的距离为d.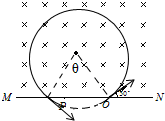 如图所示,一带电量为q=2×10-9c,质量为m=2×10-16kg的粒子,在直线上一点O沿30°角方向进入磁感应强度B=0.2T的匀强磁场中(磁场在直线上方的区域足够大),已知OP的距离为0.5m,求:
如图所示,一带电量为q=2×10-9c,质量为m=2×10-16kg的粒子,在直线上一点O沿30°角方向进入磁感应强度B=0.2T的匀强磁场中(磁场在直线上方的区域足够大),已知OP的距离为0.5m,求: