��Ŀ����
4��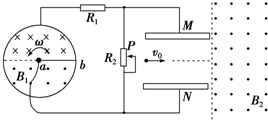 ��ͼ��ʾ���뾶ΪL1=2m�Ľ���Բ�����ϡ��°�Բ���д�ֱԲ��ƽ����н���ǿ�ų����Ÿ�Ӧǿ�ȴ�С��ΪB1=$\frac{10}{��}$ T������ҲΪL1������ΪR�Ľ�����ab��һ�˴���Բ�����ģ���һ��ǡ�ô���ڽ������ϣ�����a������ʱ�뷽������ת�������ٶ�Ϊ��=$\frac{��}{10}$ rad/s��ͨ�����߽������˵�a�˺ͽ��������ӵ�ͼʾ�ĵ�·�У�����a�˵ĵ�����Բ�����Ӵ���ͼ�еĶ�ֵ����R1=R����ƬPλ��R2�������룬R2������ֵΪ4R����ͼ�е�ƽ�а峤��ΪL2=2m������Ϊd=2m��ͼʾλ��Ϊ��ʱ��㣬��ƽ�а����Ե���봦�պ���һ���������Գ��ٶ�v0=0.5m/s�����˶�����ǡ���ܴ�ƽ�а���ұ�Ե�ɳ���֮����뵽�н���ǿ�ų��У���Ÿ�Ӧǿ�ȴ�СΪB2����߽�Ϊͼ�е�����λ�ã��Ҳ༰���·�Χ���㹻�����Խ�������Բ���ĽӴ����衢Բ�����輰���ߵ��裬���Ե������ij�ŵ�ʱ�䣬���Դ��������ڴų����˶�ʱ�ĵ�ŷ����Ӱ�죬����ƽ�н��������˵ı�ԵЧӦ���������ӵ������Ϳ�����������
��ͼ��ʾ���뾶ΪL1=2m�Ľ���Բ�����ϡ��°�Բ���д�ֱԲ��ƽ����н���ǿ�ų����Ÿ�Ӧǿ�ȴ�С��ΪB1=$\frac{10}{��}$ T������ҲΪL1������ΪR�Ľ�����ab��һ�˴���Բ�����ģ���һ��ǡ�ô���ڽ������ϣ�����a������ʱ�뷽������ת�������ٶ�Ϊ��=$\frac{��}{10}$ rad/s��ͨ�����߽������˵�a�˺ͽ��������ӵ�ͼʾ�ĵ�·�У�����a�˵ĵ�����Բ�����Ӵ���ͼ�еĶ�ֵ����R1=R����ƬPλ��R2�������룬R2������ֵΪ4R����ͼ�е�ƽ�а峤��ΪL2=2m������Ϊd=2m��ͼʾλ��Ϊ��ʱ��㣬��ƽ�а����Ե���봦�պ���һ���������Գ��ٶ�v0=0.5m/s�����˶�����ǡ���ܴ�ƽ�а���ұ�Ե�ɳ���֮����뵽�н���ǿ�ų��У���Ÿ�Ӧǿ�ȴ�СΪB2����߽�Ϊͼ�е�����λ�ã��Ҳ༰���·�Χ���㹻�����Խ�������Բ���ĽӴ����衢Բ�����輰���ߵ��裬���Ե������ij�ŵ�ʱ�䣬���Դ��������ڴų����˶�ʱ�ĵ�ŷ����Ӱ�죬����ƽ�н��������˵ı�ԵЧӦ���������ӵ������Ϳ�������������1����0��4s�ڣ�ƽ�а��ĵ��Ʋ�UMN��
��2���������ӷɳ��糡ʱ���ٶȣ�
��3��������ǰ�����������뿪�ų���ڶ��ν���糡����Ÿ�Ӧǿ��B2Ӧ�����������
���� ��1�������и�Ÿ��߲����綯�ƣ���ϴ�������·�ص㼴����⣮
��2�����������ڵ糡������ƽ���˶������˶�ѧ֪ʶ��⼴�ɣ�
��3�����������ڴų���������Բ���˶�������ţ�ٵڶ�������������˶��뾶����ϼ��ι�ϵ���ų�ǿ�ȴ�С��
��� �⣺��1�������˲����ĸ�Ӧ�綯�ƺ�Ϊ
E=$\frac{1}{2}$B1L${\;}_{1}^{2}$��=2 V
�ɴ�������·�������ص�֪��E=I•4R��U0=I•2R=$\frac{E}{2}$=1 V
T1=$\frac{2��}{��}$=20 s
�����ֶ���֪��
��0��4 sʱ���ڣ�������ab�еĵ�������Ϊb��a�����a����b������0��4 sʱ���ڣ���M����N��UMN=-1 V
��2��������ƽ�а������������ƽ���˶�����0��$\frac{{T}_{1}}{2}$ʱ����ˮƽ����L2=v0•t1
t1=$\frac{{L}_{2}}{{v}_{0}}$=4 s��$\frac{{T}_{1}}{2}$
��ֱ����$\frac{d}{2}$=$\frac{1}{2}$at${\;}_{1}^{2}$
������vy=at1=$\frac{1}{2}$m/s
��ã�a=$\frac{1}{8}$m/s2������Ϊ��a=$\frac{qE}{m}$=$\frac{qU}{md}$����ã�
$\frac{q}{m}=\frac{1}{4}$C/kg
�����ӷɳ��糡ʱ���ٶ�v=$\sqrt{{v}_{0}^{2}+{v}_{y}^{2}}$=$\frac{\sqrt{2}}{2}$m/s
tan ��=$\frac{{v}_{y}}{{v}_{0}}$=1�����Ը��ٶ���ˮƽ����ļнǦ�=45��
��3����������ǿ�ų���������Բ���˶�����B2qv=m$\frac{{v}^{2}}{r}$
��r=$\frac{mv}{{B}_{2}q}$
�ɼ��ι�ϵ�������ڴų����˶��ĶԳ��Կ�֪��
$\sqrt{2}$r��dʱ�뿪�ų���ڶ��ν���糡����B2��$\frac{\sqrt{2}mv}{dq}$=$\frac{\sqrt{2}��4}{2}$��$\frac{\sqrt{2}}{2}$=2 T
�𣺣�1����0��4s�ڣ��������ĵ��Ʋ�UMNΪ-1 V
��2���������ӷɳ��糡ʱ���ٶ�Ϊ$\frac{\sqrt{2}}{2}$m/s��������ˮƽ����ļн�Ϊ45�㡡
��3���ų�ǿ�ȴ�СB2��2 T��
���� �����Ǵ��������ڵ�ų����˶��ĵ�����Ŀ�����ú����������е��˶����ɽ����صĹ�ʽ�����ι�ϵ��⼴�ɣ�

 �����Ծ���Ԫ���Ծ�ϵ�д�
�����Ծ���Ԫ���Ծ�ϵ�д�| A�� | �о��۲���ʳʱ������̫�������ʵ� | |
| B�� | ������ת�����İ�������Ա�ɿ����ʵ� | |
| C�� | �о�һ���γ�ͨ��֦�Ǵ��ŵ�ʱ��ʱ�������ɿ����ʵ� | |
| D�� | ����10�����칬�Խ�ʱ������10�ſɿ����ʵ� |
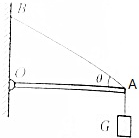 ��ͼ��ʾ��һ���ʺ��0���ý����̶���ǽ�ϣ�A������������ʹ0A�˱���ˮƽ������A�˹�һ����G���ڰ�����������A��O�����ƶ��Ĺ����У������ж�����ȷ���ǣ�������
��ͼ��ʾ��һ���ʺ��0���ý����̶���ǽ�ϣ�A������������ʹ0A�˱���ˮƽ������A�˹�һ����G���ڰ�����������A��O�����ƶ��Ĺ����У������ж�����ȷ���ǣ�������| A�� | ǽ�Ը˵�������һֱ��� | B�� | ǽ�Ը˵��������ȱ�С������ | ||
| C�� | ǽ�Ը˵��������ȱ���С | D�� | ǽ�Ը˵�����������СֵΪGcos�� |
 ��ͼ��ʾ���������������ŵ���Q1��Q2�̶���x���ϣ�����Q1�����磮������acdΪ���������Σ�cd����x�ᴹֱ����x���ཻ��b�㣬������˵����ȷ���ǣ�������
��ͼ��ʾ���������������ŵ���Q1��Q2�̶���x���ϣ�����Q1�����磮������acdΪ���������Σ�cd����x�ᴹֱ����x���ཻ��b�㣬������˵����ȷ���ǣ�������| A�� | a�㳡ǿС��b�㳡ǿ | |
| B�� | a����Ƹ���b����� | |
| C�� | �����Ӵ�a���ƶ���b�����Ƶ�c�㣬�����ܼ��� | |
| D�� | �����Ӵ�a���ƶ���c�㣬�糡�������� |
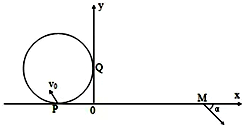 ��ͼ��ʾ����xOyƽ��ĵڢ��������а뾶ΪR��Բ�ֱ���x�ᣬy��������P��Q���㣬Բ�ڴ��ڴ�ֱ��xOyƽ���������ǿ�ų����ڵ�I�����ڴ�����y�Ḻ�������ǿ�糡���糡ǿ��ΪE��һ����������ӣ�����������������v0��P������ų���ǡ�ô�ֱy�����糡������M��3R��0��������糡�����䷽����x��������нǦ�=45�㣬������
��ͼ��ʾ����xOyƽ��ĵڢ��������а뾶ΪR��Բ�ֱ���x�ᣬy��������P��Q���㣬Բ�ڴ��ڴ�ֱ��xOyƽ���������ǿ�ų����ڵ�I�����ڴ�����y�Ḻ�������ǿ�糡���糡ǿ��ΪE��һ����������ӣ�����������������v0��P������ų���ǡ�ô�ֱy�����糡������M��3R��0��������糡�����䷽����x��������нǦ�=45�㣬������| A�� | ���������ڴų����˶��Ĺ���뾶Ϊ1.5R | |
| B�� | �ų��ĴŸ�Ӧǿ�ȴ�СΪ$\frac{2E}{{v}_{0}}$ | |
| C�� | �������ӵıȺ�Ϊ$\frac{{v}_{0}^{2}}{3RE}$ | |
| D�� | ���������˶�����y��ʱ������ֵΪR |
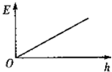
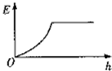
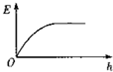
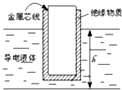 ��ͼ��ʾ�DzⶨҺ��߶�h�Ĵ��������ڵ���о������Ϳ��һ���Ե���ʣ����뵼��Һ���У��ڼ�����ϾͿ���֪��h�ı仯�������ʵ���Զ����ƣ�����˵����ȷ���ǣ�������
��ͼ��ʾ�DzⶨҺ��߶�h�Ĵ��������ڵ���о������Ϳ��һ���Ե���ʣ����뵼��Һ���У��ڼ�����ϾͿ���֪��h�ı仯�������ʵ���Զ����ƣ�����˵����ȷ���ǣ�������| A�� | Һ��߶�h����ݱ�� | |
| B�� | Һ��߶�h��С�����ݱ�� | |
| C�� | ����о�ߺ͵���Һ�幹�ɵ������������缫 | |
| D�� | ����о�ߵ�����ɵ����������缫 |
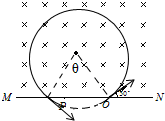 ��ͼ��ʾ��һ������Ϊq=2��10-9c������Ϊm=2��10-16kg�����ӣ���ֱ����һ��O��30��Ƿ������Ÿ�Ӧǿ��B=0.2T����ǿ�ų��У��ų���ֱ���Ϸ��������㹻����֪OP�ľ���Ϊ0.5m����
��ͼ��ʾ��һ������Ϊq=2��10-9c������Ϊm=2��10-16kg�����ӣ���ֱ����һ��O��30��Ƿ������Ÿ�Ӧǿ��B=0.2T����ǿ�ų��У��ų���ֱ���Ϸ��������㹻����֪OP�ľ���Ϊ0.5m���� ��ͼ��ʾ��һ���϶˿����¶˷�յľ���ϸ����������ֱ���ã��²��г�l1=60cm��ˮ�������м���г�l2=15cm�Ŀ��������ϲ��г�l3=25cm��ˮ��������ʱˮ����ǡ����ܿ���ƽ����֪����ѹǿΪP0=75cmHg��������������Ϊ�������壬��
��ͼ��ʾ��һ���϶˿����¶˷�յľ���ϸ����������ֱ���ã��²��г�l1=60cm��ˮ�������м���г�l2=15cm�Ŀ��������ϲ��г�l3=25cm��ˮ��������ʱˮ����ǡ����ܿ���ƽ����֪����ѹǿΪP0=75cmHg��������������Ϊ�������壬��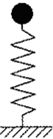 ��ͼ��ʾ����һС����ڵ����Ͼ�ֹ����������ѹС��ѹ��һ���̶Ⱥ�ȥѹ����С�����뿪���ɣ����ƿ������������������������С��Ļ�е���������߶ȵı仯ͼ�������ȷ���ǣ�������
��ͼ��ʾ����һС����ڵ����Ͼ�ֹ����������ѹС��ѹ��һ���̶Ⱥ�ȥѹ����С�����뿪���ɣ����ƿ������������������������С��Ļ�е���������߶ȵı仯ͼ�������ȷ���ǣ�������