题目内容
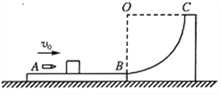
【题目】有一个竖直固定放置的四分之一光滑圆弧轨道，轨道圆心O到地面的高度为h，小球从轨道最高点A由静止开始沿着圆弧轨道滑下，从轨道最低点B离开轨道，然后做平抛运动落到水平地面上的C点，C点与A点的水平距离也等于h，则下列说法正确的是
A. 当小球运动到轨道最低点B时，轨道对它的支持力等于重力的4倍
B. 小球在圆弧轨道上运动的过程中，重力对小球的冲量在数值上大于圆弧的支持力对小球的冲量
C. 根据已知条件可以求出该四分之一圆弧轨道的轨道半径为0.2h
D. 小球做平抛运动落到地面时的速度与水平方向夹角θ的正切值tanθ=0.5
【答案】C
【解析】A、在最低点
，
，解得FB =3mg，A错误；B、小球从A运动到B，合外力冲量水平向右，则支持力的冲量在竖直方向的分量与重力的冲量大小相等，故支持力冲量在数值上大于重力的冲量，B错误；C、小球做平抛运动时，
，
，解得R=0.2h，C正确；D、设小球做平抛运动位移与水平方向夹角为α，则tanα=1，因为tanθ =2tanα，所以tanθ=2,D错误.故选C.
练习册系列答案
名校课堂系列答案
相关题目
