题目内容
【题目】如图所示,长木板AB和光滑四分之一圆弧轨道在B点平滑连接成一个整体,放置在光滑的水平面上,长木板和圆弧轨道的总质量为M=3kg,一个质量为m=0.98kg的物块放在木板AB的中点,一颗质量为m0=20g的子弹以初速度v0=100m/s射入物块并留在物块中(子弹射入物块时间极短,可忽略不计),木板的长度L=1m,重力加速度取g=10m/s2.
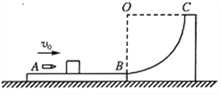
(1)要使物块能滑上圆弧轨道,物块与长木板间的动摩擦因数应该满足什么条件?
(2)若物块与长木板间的动摩擦因数为μ=0.15,物块从子弹击中后到运动至B点,需要多长时间?
【答案】(1)小于0.3 (2)![]()
【解析】(1)子弹射入物块过程,根据动量守恒定律有:m0v0=(m0+m)v1
求得v1=2m/s
若物块刚好滑到B点时与木板有共同速度,则:(m0+m)v1=( m0+m +M) v2
求得v2=0.5m/s
根据功能关系:![]()
求得:μ=0.3
因此,要使物块能滑上圆弧轨道,物块与长木板间的动摩擦因数应小于0.3
(2)设物块到达B点时,物块和木板与圆弧轨道组成的整体各自的速度分别是va、vb,需要的时间为t.
对物块,由动量定理得:-μ(m+m0)gt=m(m+m0) va-(m+m0) v1
对木板和圆弧轨道,由动量定理得μ(m+m0)gt=Mvb
物块滑到B点时,有![]()
可解得![]() ,另一解不符合题意,舍去。
,另一解不符合题意,舍去。
因木板和圆弧轨道在物块上升到最高点时的速度为0.5m/s,

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目