题目内容
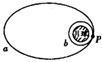
“重力勘探”是应用地球表面某处重力加速度的异常来寻找矿床的一种技术.如图所示,若在地球表面A处正下方有一均匀分布且半径为R球形矿床,球心与A相距r.矿床的密度为nρ(n>1,ρ为地球的平均密度),万有引力常量为G.则仅由于该矿床的存在,A处的重力加速度的变化量△g为( )

A.△g=
| B.△g=
| ||||
C.△g=
| D.
|

矿床对对表面物质的吸引力 F1=
(M1是矿床的质量).
如果将矿床替换为普通地球的物质 则 这个普通物质对地球表面物质的吸引力
F2=
(M2是普通物质的质量).
那么这时在有矿床的地方的重力加速度 mg矿=mg-F2+F1
所以m(g矿-g)=F1-F2=
得△g=g矿-g=
由于 矿床的密度为nρ
所以M1=
而M2=
(ρ是地球平均密度)
所以△g=
.故A正确,B、C、D错误.
故选A.
| GM1m |
| r2 |
如果将矿床替换为普通地球的物质 则 这个普通物质对地球表面物质的吸引力
F2=
| GM2m |
| r2 |
那么这时在有矿床的地方的重力加速度 mg矿=mg-F2+F1
所以m(g矿-g)=F1-F2=
| G(M1-M2)m |
| r2 |
得△g=g矿-g=
| G(M1-M2) |
| r2 |
由于 矿床的密度为nρ
所以M1=
| 4πR3nρ |
| 3 |
而M2=
| 4πR3ρ |
| 3 |
所以△g=
| 4πR3(n-1)Gρ |
| 3r2 |
故选A.

练习册系列答案
相关题目
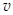 和运行周期T卫
和运行周期T卫