题目内容
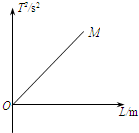 在“用单摆测定重力加速度”的实验中:
在“用单摆测定重力加速度”的实验中:①甲同学分别选用三种材料不同、直径2cm的实心球做实验,各组实验的测量数据如下表.若要计算当地的重力加速度,应选用第
3
3
组实验数据.| 组别 | 摆球材料 | 摆长L/m | 最大摆角 | 全振动次数N/次 | 测量时间t/s |
| 1 | 铜 | 0.30 | 5° | 50 | 55.1 |
| 2 | 铜 | 1.00 | 5° | 1 | 1.8 |
| 3 | 铁 | 1.00 | 5° | 50 | 100.3 |
| 4 | 木 | 1.00 | 5° | 10 | 21.2 |
| 4π2 |
| k |
| 4π2 |
| k |
③丙、丁两同学合作测量重力加速度,测出一组数据.丙用T2-L图象法处理求得重力加速度为g丙;丁用公式法T=2π
|
>
>
g 丁(填“>”“<”“=”)分析:(1)单摆应选择密度较大、直径较小的材料做成的小球作为摆球.采用累积法测量单摆的周期.摆线长度大约1m左右,振动较慢,便于测量时间.
(2)根据单摆的周期公式和数学知识得到重力加速度与T2-L图象斜率的关系.
(3)根据重力加速度的表达式分析丙、丁两同学实验的误差,再比较测量值的大小.
(2)根据单摆的周期公式和数学知识得到重力加速度与T2-L图象斜率的关系.
(3)根据重力加速度的表达式分析丙、丁两同学实验的误差,再比较测量值的大小.
解答:解:(1)应选用第3组实验数据.因为第1组:摆长太短,单摆周期太小,测量周期引起的误差较大,也不便于测量.第2组:把单摆一次振动的时间作为周期,误差太大.第4组选木球作为摆球,空气阻力影响较大.
(2)根据重力加速度的表达式g=
可知,T2-l图线斜率k=
,则g=
.
(3)丙用T2-L图象法处理求得重力加速度为g丙,测摆长时忘了加上摆球的半径,图线与加上摆球的半径的图线平行,斜率相同,重力加速度相同.而丁用公式法T=2π
处理求得重力加速度为g丁,测摆长时忘了加上摆球的半径,则测得g丁偏小.所以g丙>g 丁.
故答案为:(1)3;(2)
;(3)>
(2)根据重力加速度的表达式g=
| 4π2L |
| T2 |
| 4π2 |
| g |
| 4π2 |
| k |
(3)丙用T2-L图象法处理求得重力加速度为g丙,测摆长时忘了加上摆球的半径,图线与加上摆球的半径的图线平行,斜率相同,重力加速度相同.而丁用公式法T=2π
|
故答案为:(1)3;(2)
| 4π2 |
| k |
点评:本题考查对单摆选材、实验方法和数据处理的能力.对于实验误差,关键从实验原理分析.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
在《用单摆测定重力加速度》的实验中,某同学测出的g值比当地值大,造成的原因可能是( )
| A、摆角太大了(摆角仍小于10°) | B、量摆长时从悬点量到球的最下端 | C、计算摆长时忘记把小球半径加进去 | D、摆球不是在竖直平面内做简谐振动,而是做圆锥摆运动 | E、计算周期时,将(n-1)次全振动误记为n次全振动 |
 某实验小组在进行“用单摆测定重力加速度”的实验中,已知单摆在摆动过程中的摆角小于5°;在测量单摆的周期时,从单摆运动到最低点开始计时且记数为1,到第n次经过最低点所用的时间内为t;在测量单摆的摆长时,先用毫米刻度尺测得悬挂后的摆线长(从悬点到摆球的最上端)为L,再用游标卡尺测得摆球的直径为d.
某实验小组在进行“用单摆测定重力加速度”的实验中,已知单摆在摆动过程中的摆角小于5°;在测量单摆的周期时,从单摆运动到最低点开始计时且记数为1,到第n次经过最低点所用的时间内为t;在测量单摆的摆长时,先用毫米刻度尺测得悬挂后的摆线长(从悬点到摆球的最上端)为L,再用游标卡尺测得摆球的直径为d. 某实验小组在进行“用单摆测定重力加速度”的实验中,已知单摆摆动过程中的摆角小于5°;在测量单摆的周期时,从单摆运动到最低点开始计时且记数为1,到第n次经过最低点所用的时间内为t;在测量单摆的摆长时,先用毫米刻度尺测得悬挂后的摆线长(从悬点到摆球的最上端)为L,再用游标卡尺测得摆球的直径为d.
某实验小组在进行“用单摆测定重力加速度”的实验中,已知单摆摆动过程中的摆角小于5°;在测量单摆的周期时,从单摆运动到最低点开始计时且记数为1,到第n次经过最低点所用的时间内为t;在测量单摆的摆长时,先用毫米刻度尺测得悬挂后的摆线长(从悬点到摆球的最上端)为L,再用游标卡尺测得摆球的直径为d.