题目内容
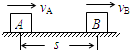如图所示，A、B两物体相距s=7m，物体A以vA=4m/s 的速度向右匀速运动，而物体B此时的速度vB=10m/s，只在摩擦力作用下向右做匀减速运动，加速度a=-2m/s2，那么物体A追上物体B所用的时间为（ ）分析：假设经过时间t，物块A追上物体B，根据位移时间公式结合几何关系列式求解即可．
解答：解：物体A做匀速直线运动，位移为：xA=vAt=4t
物体B做匀减速直线运动减速过程的位移为：xB=vBt+
at2=10t-t2
设物体B速度减为零的时间为t1，有t1=
=5s
在t1=5s的时间内，物体B的位移为xB1=25m，物体A的位移为xA1=20m，由于xA1+S＞xB1，故物体A未追上物体B；
5s后，物体B静止不动，故物体A追上物体B的总时间为：t总=
=
s=8s
故选B．
物体B做匀减速直线运动减速过程的位移为：xB=vBt+
| 1 |
| 2 |
设物体B速度减为零的时间为t1，有t1=
| 0-vB |
| a |
在t1=5s的时间内，物体B的位移为xB1=25m，物体A的位移为xA1=20m，由于xA1+S＞xB1，故物体A未追上物体B；
5s后，物体B静止不动，故物体A追上物体B的总时间为：t总=
| xA1+S |
| vA |
| 25+7 |
| 4 |
故选B．
点评：本题是追击问题，特别要注意物体B做匀减速运动，要分清是减速过程追上还是静止后被追上；第二种情况下的位移用位移时间公式求解时要注意时间是减速的时间，而不是总时间．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
点睛新教材全能解读系列答案
相关题目
如图所示，A、B两物块质量均为m，用一轻弹簧相连，将A用长度适当的轻绳悬挂于天花板上，系统处于静止状态，B物块恰好与水平桌面接触，此时轻弹簧的伸长量为x，弹簧的弹性势能为Ep，现将悬绳剪断，已知同一弹簧的弹性势能仅与形变量大小有关，且弹簧始终在弹性限度内，则在以后的运动过程中（ ）
（2011?天津）如图所示，A、B两物块叠放在一起，在粗糙的水平面上保持相对静止地向右做匀减速直线运动，运动过程中B受到的摩擦力（ ）
如图所示，a、b 两物块质量分别为 m、2m，用不计质量的细绳相连接，悬挂在定滑轮的两侧，不计滑轮质量和一切摩擦．开始时，a、b 两物块距离地面高度相同，用手托住物块 b，然后突然由静止释放，直至 a、b 物块间高度差为 h．在此过程中，下列说法正确的是（ ）
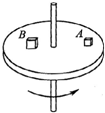如图所示，A、B两物块置于绕竖直轴匀速转动的水平圆盘上，两物块始终相对圆盘静止，已知两物块的质量mA＜mB，运动半径rA＞rB，则下列关系一定正确的是（ ）| A、角速度ωA=ωB | B、线速度vA=vB | C、向心加速度aA＞aB | D、向心力FA＞FB |
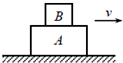如图所示，A、B两物块叠放在一起，在粗糙的水平面上保持相对静止地向右做匀减速直线运动，运动过程中A受到B对它的摩擦力（ ）| A、方向向左，大小不变 | B、方向向左，逐渐减小 | C、方向向右，大小不变 | D、方向向右，逐渐减小 |