题目内容
5.在中国航天骄人的业绩中有这些记载:“天宫二号”在离地面343km的圆形轨道上飞行;“嫦娥三号”在距月球表面高度为200km的圆形轨道上飞行;“北斗”卫星导航系统由“同步卫星”(地球静止轨道卫星,在赤道平面,距赤道的高度约为 36000千米)和“倾斜同步卫星”(周期与地球自转周期相等,但不定点于某地上空)等组成.则以下分析正确的是( )| A. | 设“天宫二号”绕地球运动的周期为T,用G表示引力常量,则用表达式ρ=$\frac{3π}{G{T}^{2}}$求得的地球平均密度比真实值要小 | |
| B. | “天宫二号”的飞行速度比“同步卫星”的飞行速度要大 | |
| C. | “同步卫星”和“倾斜同步卫星”同周期、同轨道半径,但两者的轨道平面不在同一平面内 | |
| D. | “嫦娥三号”与地球的距离比“同步卫星”与地球的距离小 |
分析 卫星绕地球做匀速圆周运动,根据万有引力提供向心力可以表示出地球质量,根据密度公式表示出密度判断.
根据万有引力提供向心力可以表示出线速度,根据轨道半径的关系判断飞行速度大小.
根据“同步卫星”和“倾斜同步卫星”的特点求解.
解答 解:A、卫星绕地球做匀速圆周运动,根据万有引力提供向心力:$\frac{GMm}{{r}^{2}}$=$\frac{m•4{π}^{2}r}{{T}^{2}}$
则有:M=$\frac{4{π}^{2}{r}^{3}}{G{T}^{2}}$
根据密度公式得地球平均密度ρ=$\frac{M}{V}$=$\frac{3π{r}^{3}}{G{T}^{2}{R}^{3}}$,
由于天宫一号的轨道半径r大于地球半径R,所以用表达式$\frac{3π}{G{T}^{2}}$ 求得的地球平均密度比真实值要小,故A正确;
B、卫星绕地球做匀速圆周运动,根据万有引力提供向心力,$\frac{GMm}{{r}^{2}}$=$\frac{m{v}^{2}}{r}$
则有:v=$\sqrt{\frac{GM}{r}}$,“天宫一号”的轨道半径比“同步卫星”的要小,所以“天宫一号”的飞行速度比“同步卫星”的飞行速度要大,故B正确;
C、“同步卫星”和“倾斜同步卫星”的周期都是24小时.所以同周期、同轨道半径,“同步卫星”定点在赤道正上方,“倾斜同步卫星”不定点于某地上空,但两者的轨道平面不在同一平面内.故C正确;
D、“嫦娥三号”在距月球表面高度为200km的圆形轨道上飞行;“同步卫星”绕地球运动,所以“嫦娥三号”与地球的距离比“同步卫星”与地球的距离大,故D错误;
故选:ABC
点评 本题考查了地球卫星轨道相关知识点,地球卫星围绕地球做匀速圆周运动,圆心是地球的地心,万有引力提供向心力,轨道的中心一定是地球的球心.

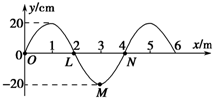 某横波在介质中沿x轴正方向传播,t=0时刻,O点开始向正方向运动,经t=0.2s,O点第一次到达正方向最大位移处,某时刻形成的波形如图所示,正确的是( )
某横波在介质中沿x轴正方向传播,t=0时刻,O点开始向正方向运动,经t=0.2s,O点第一次到达正方向最大位移处,某时刻形成的波形如图所示,正确的是( )| A. | 该横波的波速为5 m/s | |
| B. | 该波形图可能是t=1.2 s时刻的 | |
| C. | 质点L与质点N都运动起来后,它们的运动方向总相反 | |
| D. | 在0.2 s的时间内质点M通过的路程为20c m | |
| E. | 在t=2.6 s时刻,质点M处于平衡位置,正沿y轴正方向运动 |

| A. | 电压表读数变大,通过灯L1的电流变大,灯L2变亮 | |
| B. | 电压表读数变小,通过灯L1的电流变小,灯L2变暗 | |
| C. | 电压表读数变大,通过灯L2的电流变小,灯L1变暗 | |
| D. | 电压表读数变小,通过灯L2的电流变大,灯L1变暗 |

| A. | 甲在4s时间内做匀变速直线运动 | |
| B. | 乙在t=2s时运动方向发生改变 | |
| C. | 乙在4s时间内通过的总位移大小为0 | |
| D. | 甲在4s时间内有往返运动,它通过的总路程为6m |
 一物体做直线运动,其v-t图象如图所示,从图中可以看出,以下说法正确的是( )
一物体做直线运动,其v-t图象如图所示,从图中可以看出,以下说法正确的是( )| A. | 0~2s和5~6s内加速度的方向与速度方向均相同 | |
| B. | 4~5s内物体的加速度为3m/s2 | |
| C. | 4~6s 内物体的速度一直在减小 | |
| D. | 只有0~2s内加速度与速度方向相同 |
| A. | 超声波被血流反射回来其频率发生变化可测血流速度,这是利用多普勒效应 | |
| B. | 空间中某个区域有变化的电场或变化的磁场,不一定能产生电磁波 | |
| C. | 部队过桥不能齐步走而要便步走,是为了避免桥梁发生共振现象 | |
| D. | 用标准平面来检查光学面的平整程度是利用光的衍射现象 |

