题目内容
13.物体甲的速度与时间图象和物体乙的位移与时间图象分别如图所示,则这两个物体的运动情况是( )
| A. | 甲在4s时间内做匀变速直线运动 | |
| B. | 乙在t=2s时运动方向发生改变 | |
| C. | 乙在4s时间内通过的总位移大小为0 | |
| D. | 甲在4s时间内有往返运动,它通过的总路程为6m |
分析 v-t图象的斜率表示加速度,与t轴包围的面积表示位移大小;x-t图象的斜率表示速度,面积无意义.根据两图象的性质进行分析,从而明确对应的物理规律.
解答 解:A、v-t图象的斜率表示加速度,甲在4s时间内的v-t图象是直线,加速度恒定不变,做匀变速直线运动,故A正确;
B、x-t图象的斜率表示速度,乙图表示物体做匀速直线运动,2s时物体的速度方向并没有发生变化,故B错误;
C、乙在4s时间内从-3m运动到+3m位置,故位移大小为6m,故C错误;
D、甲在4s内先反向减速,位移x1=$\frac{1}{2}×2×3$=3m;又正向加速,位移x2=$\frac{1}{2}×2×3$=3m,故总路程为S=x1+x2=3+3=6m;故D正确.
故选:AD.
点评 本题考查了x-t图象与v-t图象的区别,要注意两图象的性质不同,明确v-t图象中斜率、与t轴包围的面积的含义以及x-t图象中的斜率意义.

练习册系列答案
相关题目
3.一列沿x轴正方向传播的简谐横波,周期为0.50s.某一时刻,离开平衡位置的位移都相等的各质点依次为P1,P2,P3,….已知P1和P2之间的距离为20cm,P2和P3之间的距离为80cm,则P1的振动传到P2所需的时间为( )
| A. | 0.10 s | B. | 0.13 s | C. | 0.20 s | D. | 0.50 s |
4.关于静电场的等势面和电场线,下列说法正确的是( )
| A. | 两个电势不同的等势面可能相交 | |
| B. | 沿着电场线线方向电势逐渐升高 | |
| C. | 同一等势面上各点电场强度一定相等 | |
| D. | 将一正的试探电荷从电势较高的等势面移至电势较低的等势面,电场力做正功 |
1.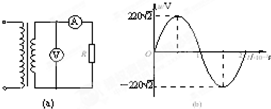 如图(a)中的理想变压器输入如图(b)所示正弦交变电流,电路中电阻R=55Ω,交流电流表、交流电压表均为理想电表.若原、副线圈匝数比为2:1,下列正确的是( )
如图(a)中的理想变压器输入如图(b)所示正弦交变电流,电路中电阻R=55Ω,交流电流表、交流电压表均为理想电表.若原、副线圈匝数比为2:1,下列正确的是( )
 如图(a)中的理想变压器输入如图(b)所示正弦交变电流,电路中电阻R=55Ω,交流电流表、交流电压表均为理想电表.若原、副线圈匝数比为2:1,下列正确的是( )
如图(a)中的理想变压器输入如图(b)所示正弦交变电流,电路中电阻R=55Ω,交流电流表、交流电压表均为理想电表.若原、副线圈匝数比为2:1,下列正确的是( )| A. | 电压表的示数为110V | B. | 原线圈输入功率为440W | ||
| C. | 通过电阻R的电流的频率为25Hz | D. | 电流表的示数为2A |
8.关于速度和加速度,下列说法中正确的是( )
| A. | 物体的速度增大,加速度一定增大 | |
| B. | 物体的速度很大,加速度可能为零 | |
| C. | 物体加速度的方向一定与速度方向一致 | |
| D. | 物体加速度的方向与速度变化的方向相同 |
5.在中国航天骄人的业绩中有这些记载:“天宫二号”在离地面343km的圆形轨道上飞行;“嫦娥三号”在距月球表面高度为200km的圆形轨道上飞行;“北斗”卫星导航系统由“同步卫星”(地球静止轨道卫星,在赤道平面,距赤道的高度约为 36000千米)和“倾斜同步卫星”(周期与地球自转周期相等,但不定点于某地上空)等组成.则以下分析正确的是( )
| A. | 设“天宫二号”绕地球运动的周期为T,用G表示引力常量,则用表达式ρ=$\frac{3π}{G{T}^{2}}$求得的地球平均密度比真实值要小 | |
| B. | “天宫二号”的飞行速度比“同步卫星”的飞行速度要大 | |
| C. | “同步卫星”和“倾斜同步卫星”同周期、同轨道半径,但两者的轨道平面不在同一平面内 | |
| D. | “嫦娥三号”与地球的距离比“同步卫星”与地球的距离小 |
2.一辆汽车以20m/s的速度沿平直的公路从甲地开往乙地,又以30m/s的速度从乙地开往丙地.已知甲、乙两地间的距离与乙、丙两地间的距离相等,该汽车在从甲地开往丙地的过程中平均速度的大小为( )
| A. | 22 m/s | B. | 24 m/s | C. | 25m/s | D. | 28 m/s |
3. 在2016年6月1日,总参组织实施的”跨越-2016朱日和”系列实兵对抗军事演习中,某空降兵从飞机上跳下,先做自由落体运动,在t1时刻,速度达较大值v1时打开降落伞,做减速运动,在t2时刻以较小速度v2着地.他的速度图象如图所示.下列关于该空降兵在0~t1或t1~t2时间内的平均速度$\overline v$的结论正确的是( )
在2016年6月1日,总参组织实施的”跨越-2016朱日和”系列实兵对抗军事演习中,某空降兵从飞机上跳下,先做自由落体运动,在t1时刻,速度达较大值v1时打开降落伞,做减速运动,在t2时刻以较小速度v2着地.他的速度图象如图所示.下列关于该空降兵在0~t1或t1~t2时间内的平均速度$\overline v$的结论正确的是( )
 在2016年6月1日,总参组织实施的”跨越-2016朱日和”系列实兵对抗军事演习中,某空降兵从飞机上跳下,先做自由落体运动,在t1时刻,速度达较大值v1时打开降落伞,做减速运动,在t2时刻以较小速度v2着地.他的速度图象如图所示.下列关于该空降兵在0~t1或t1~t2时间内的平均速度$\overline v$的结论正确的是( )
在2016年6月1日,总参组织实施的”跨越-2016朱日和”系列实兵对抗军事演习中,某空降兵从飞机上跳下,先做自由落体运动,在t1时刻,速度达较大值v1时打开降落伞,做减速运动,在t2时刻以较小速度v2着地.他的速度图象如图所示.下列关于该空降兵在0~t1或t1~t2时间内的平均速度$\overline v$的结论正确的是( )| A. | 0~t1:$\overline v=\frac{v_1}{2}$ | B. | t1~t2:$\overline v=\frac{{{v_1}+{v_2}}}{2}$ | ||
| C. | t1~t2:$\overline v<\frac{{{v_1}+{v_2}}}{2}$ | D. | t1~t2:$\overline v>\frac{{{v_1}+{v_2}}}{2}$ |