题目内容
如图甲所示,M、N为竖直放置的两块平行金属板,圆形虚线为与N相连且接地的圆形金属网罩(不计电阻).PQ为与圆形网罩同心的金属收集屏,通过阻值为r0的电阻与大地相连.小孔s1、s2、圆心O与PQ中点位于同一水平线上.圆心角2θ=120°、半径为R的网罩内有大小为B,方向垂直纸面向里的匀强磁场.M、N间相距
且接有如图乙所示的随时间t变化的电压,UMN=U0sin
t(0≤t≤T),UMN=U0(t>T)(式中U0=
,T已知),质量为m电荷量为e的质子连续不断地经s1进入M、N间的电场,接着通过s2进入磁场.(质子通过M、N的过程中,板间电场可视为恒定,质子在s1处的速度可视为零,质子的重力及质子间相互作用均不计.)
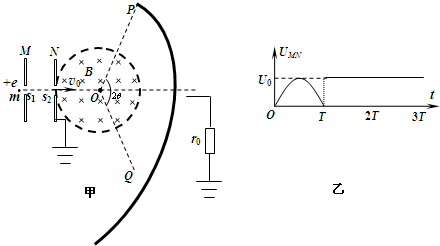
(1)若质子在t>T时刻进入s1,为使质子能打到收集屏的中心需在圆形磁场区域加上一个匀强电场,求所加匀强电场的大小和方向?
(2)质子在哪些时间段内自s1处进入板间,穿出磁场后均能打到收集屏PQ上?
(3)若毎秒钟进入s1的质子数为n,则收集屏PQ电势稳定后的发热功率为多少?
| R |
| 2 |
| π |
| T |
| 3eB2R2 |
| m |

(1)若质子在t>T时刻进入s1,为使质子能打到收集屏的中心需在圆形磁场区域加上一个匀强电场,求所加匀强电场的大小和方向?
(2)质子在哪些时间段内自s1处进入板间,穿出磁场后均能打到收集屏PQ上?
(3)若毎秒钟进入s1的质子数为n,则收集屏PQ电势稳定后的发热功率为多少?
分析:(1)质子能打到收集屏的中心,就是质子做匀速直线运动,由动能定理和受力平衡即可解得;
(2)若质子能打在收集屏上,轨道半径r与半径R应满足r≥
R,根据半径关系和动能定理即可求解;
(3)收集屏上电荷不再增加,即在t>T 时刻以后,此时,UMN=U0,收集屏与地面电势差恒为U,根据能量守恒和焦耳定律即可求解.
(2)若质子能打在收集屏上,轨道半径r与半径R应满足r≥
| 3 |
(3)收集屏上电荷不再增加,即在t>T 时刻以后,此时,UMN=U0,收集屏与地面电势差恒为U,根据能量守恒和焦耳定律即可求解.
解答: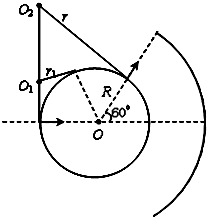 解:(1)在电场中,由动能定理得
解:(1)在电场中,由动能定理得
eU0=
mv02
为使质子做匀速直线运动,有
eE=ev0B
解得E=
方向竖直向下
(2)质子在板间运动,根据动能定理,有
eUMN=
mv02-0
质子在磁场中运动,根据牛顿第二定律,有 evB=
若质子能打在收集屏上,轨道半径r与半径R应满足的关系:
r≥
R
解得 UMN≥
结合图象可知:质子在
≤t≤
和t≥T之间任一时刻从s1处进入电场,均能打到收集屏上;
(3)稳定时,收集屏上电荷不再增加,即在t>T 时刻以后,此时,UMN=U0,收集屏与地面电势差恒为U,U=Ir0
单位时间到达收集板的质子数n
单位时间内,质子的总能量为 P总=
nmv02=neU0=IU0
单位时间内屏上发热功率为 P屏=P总-P热
消耗在电阻上的功率为 P热=I2r0
所以收集屏发热功率 P屏=P总-P热=IU0-I2r0=neU0-n2e2r0
答:所加匀强电场的大小为
和方向竖直向下;质子在
≤t
和t≥T之间任一时刻内自s1处进入板间,穿出磁场后均能打到收集屏PQ上;收集屏PQ电势稳定后的发热功率为neU0-n2e2r0.
 解:(1)在电场中,由动能定理得
解:(1)在电场中,由动能定理得eU0=
| 1 |
| 2 |
为使质子做匀速直线运动,有
eE=ev0B
解得E=
| ||
| m |
方向竖直向下
(2)质子在板间运动,根据动能定理,有
eUMN=
| 1 |
| 2 |
质子在磁场中运动,根据牛顿第二定律,有 evB=
| mv02 |
| r |
若质子能打在收集屏上,轨道半径r与半径R应满足的关系:
r≥
| 3 |
解得 UMN≥
| 3eB2R2 |
| 2m |
结合图象可知:质子在
| T |
| 6 |
| 5T |
| 6 |
(3)稳定时,收集屏上电荷不再增加,即在t>T 时刻以后,此时,UMN=U0,收集屏与地面电势差恒为U,U=Ir0
单位时间到达收集板的质子数n
单位时间内,质子的总能量为 P总=
| 1 |
| 2 |
单位时间内屏上发热功率为 P屏=P总-P热
消耗在电阻上的功率为 P热=I2r0
所以收集屏发热功率 P屏=P总-P热=IU0-I2r0=neU0-n2e2r0
答:所加匀强电场的大小为
| ||
| m |
| T |
| 6 |
| 5T |
| 6 |
点评:此类题目比较综合,关键是挖掘题目的条件,将运动状态及过程弄清楚,然后根据每个运动的规律分别进行分析,然后得出结论.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

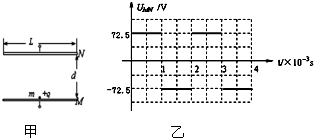 如图甲所示,M、N为水平放置的平行板电容器的两极板,极板长L=0.2m,两板间距d=0.145m,在M、N间加上如图乙所示的电压,一个带电粒子的电量q=+1.0×10-6C、质量m=1.0×10-8kg,粒子重力不计.
如图甲所示,M、N为水平放置的平行板电容器的两极板,极板长L=0.2m,两板间距d=0.145m,在M、N间加上如图乙所示的电压,一个带电粒子的电量q=+1.0×10-6C、质量m=1.0×10-8kg,粒子重力不计. (2012?嘉兴二模)如图甲所示,M、N为竖直放置的两块平行金属板,圆形虚线为与N相连且接地的圆形金属网罩.PQ为与圆形网罩同心的金属收集屏,通过阻值为r0的电阻与大地相连.小孔s1、s2、圆心O与PQ中点位于同一水平线上.圆心角2θ=120°、半径为R的网罩内有大小为B,方向垂直纸面向里的匀强磁场.M、N间相距
(2012?嘉兴二模)如图甲所示,M、N为竖直放置的两块平行金属板,圆形虚线为与N相连且接地的圆形金属网罩.PQ为与圆形网罩同心的金属收集屏,通过阻值为r0的电阻与大地相连.小孔s1、s2、圆心O与PQ中点位于同一水平线上.圆心角2θ=120°、半径为R的网罩内有大小为B,方向垂直纸面向里的匀强磁场.M、N间相距