题目内容
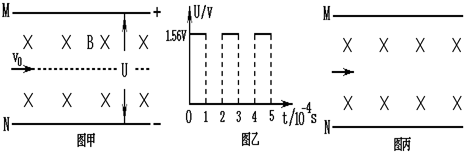
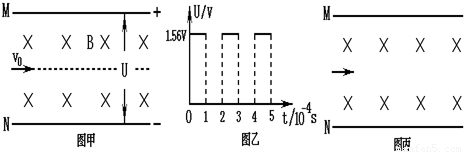
如图甲所示,M和N为水平放置的金属板,板长L=1.4m,板间距离d=0.3m.两板间有匀强磁场,磁感应强度B=1.3×10-3T.现在MN之间加上按图乙变化的电压.现有一束a粒子从两板的中间轴线以v0射入,已知v0=4×103m/s,ma=6.5×10-27kg,qa=3.2×10-19,(不计粒子的重力,π取3.2)试问:
(1)a粒子能否穿过金属板间?若能穿过,所需时间多少?
(2)a粒子的运动轨迹怎样?(在图丙中画出轨迹图)

(1)a粒子能否穿过金属板间?若能穿过,所需时间多少?
(2)a粒子的运动轨迹怎样?(在图丙中画出轨迹图)

分析:MN之间没有电场时,带电粒子受到洛伦兹力的作用,MN之间有电场时,带电粒子受到电场力与洛伦兹力的共同作用.根据它的受力,确定出带电粒子的运动的规律,代人半径公式与周期公式中,计算出对应的结果.
解答:解:(1)MN之间有电场时,带电粒子受到电场力与洛伦兹力的共同作用.
其中:F电=qaE=
=
=1.66×10-18N
洛伦兹力:F洛=qav0B=3.2×10-19×4×103×1.3×10-3=1.66×10-18N
所以存在电场时,带电粒子做匀速直线运动,没有电场时带电粒子做匀速圆周运动.
1×10-4s内带电粒子的位移:x1=v0t=0.4m<1.4m
带电粒子做匀速圆周运动的半径:qav0B=
则:r=
=
=6.25×10-2m<
=0.75m
所以带电粒子不会碰到上下极板.
带电粒子在磁场中的周期:T=
=
=1×10-4s
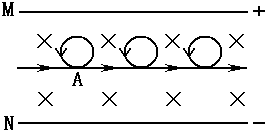
所以带电粒子运动的轨迹如图.
整个运动的总时间:t=3T+
=3×10-4s+
s=6.5×10-4s.
(2)其整个运动的轨迹如图所示.
答:(1)a粒子能穿过金属板间,所需时间6.5×10-4s.(2)a粒子的运动轨迹如图.
其中:F电=qaE=
| qaU |
| d |
| 3.2×10-19×1.56 |
| 0.3 |
洛伦兹力:F洛=qav0B=3.2×10-19×4×103×1.3×10-3=1.66×10-18N
所以存在电场时,带电粒子做匀速直线运动,没有电场时带电粒子做匀速圆周运动.
1×10-4s内带电粒子的位移:x1=v0t=0.4m<1.4m
带电粒子做匀速圆周运动的半径:qav0B=
m
| ||
| r |
则:r=
| mv0 |
| qB |
| 6.5×10-27×4×103 |
| 3.2×10-19×1.3×10-3 |
| d |
| 4 |
所以带电粒子不会碰到上下极板.
带电粒子在磁场中的周期:T=
| 2πm |
| qaB |
| 2×3.2×6.5×10-27 |
| 1.3×10-3×3.2×10-19 |
所以带电粒子运动的轨迹如图.

整个运动的总时间:t=3T+
| L |
| v0 |
| 1.4 |
| 4×103 |
(2)其整个运动的轨迹如图所示.
答:(1)a粒子能穿过金属板间,所需时间6.5×10-4s.(2)a粒子的运动轨迹如图.
点评:本题的解题关键是判断出带电粒子先做匀速直线运动,再做匀速圆周运动,并画出粒子运动的轨迹.题目的难度较大.

练习册系列答案
相关题目