题目内容
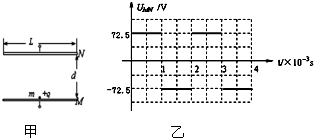 如图甲所示,M、N为水平放置的平行板电容器的两极板,极板长L=0.2m,两板间距d=0.145m,在M、N间加上如图乙所示的电压,一个带电粒子的电量q=+1.0×10-6C、质量m=1.0×10-8kg,粒子重力不计.
如图甲所示,M、N为水平放置的平行板电容器的两极板,极板长L=0.2m,两板间距d=0.145m,在M、N间加上如图乙所示的电压,一个带电粒子的电量q=+1.0×10-6C、质量m=1.0×10-8kg,粒子重力不计.(1)若在t=0的时刻,将上述带电粒子从紧临M板中心处无初速释放,求粒子从M板运动到N板所经历的时间t;
(2)若在t=0的时刻,上述带电粒子从靠近M板的左边缘处以初速度v0水平射入两极板间,且粒子沿水平方向离开电场,求初速度v0的大小.
分析:(1)带电粒子在电场中做直线运动,可能在半个周期内到达N板,否则,每半周期内的位移相等;
(2)带电粒子从靠近M板的左边缘处以初速度v0水平射入两极板间,且粒子沿水平方向离开电场,说明了两点:运动的时间是周期的整数倍,没打到极板上.根据以上两点,列出公式,即可解答.
(2)带电粒子从靠近M板的左边缘处以初速度v0水平射入两极板间,且粒子沿水平方向离开电场,说明了两点:运动的时间是周期的整数倍,没打到极板上.根据以上两点,列出公式,即可解答.
解答:解:(1)带电粒子在电场中 受到的电场力:F=qE=
它的加速度:a=
,
半个周期内的位移:x=
at2
代入数据,得:x=2.5×10-2m
因此,粒子在半周期内不能达到N板,后半周期内它做减速运动,且t=T时,速度恰好为0,之后重复该周期内的运动,直到达到N极板.
又
=
=5.8
故时间t应在2.5T到3T之间,2.5T后,粒子做减速运动,x′=d-5.5×2x=0.02m
粒子的加速度大小也是a,由公式:x′=vt+
at2
得:x′=a
?t′-
at′2
代入数据,解得:t′=5.53×10-4s
总时间为:t总=2.5T+t′=5.553×10-3s
(2)由题意得,运动的时间是周期的整数倍,没打到极板上.粒子在电场中做加速-减速运动,没打到极板上,说明沿着电场线方向的位移不超过
,故运动的时间也不
,合适的时间点只有当t=T的时候,即粒子穿越电场的时间为T,由公式得:L=v0T
解得:v0=100m/s
答:(1)粒子从M板运动到N板所经历的时间是5.553×10-3;
(2)粒子沿水平方向离开电场,求初速度v0的大小为100m/s.
| qU |
| d |
它的加速度:a=
| F |
| m |
半个周期内的位移:x=
| 1 |
| 2 |
代入数据,得:x=2.5×10-2m
因此,粒子在半周期内不能达到N板,后半周期内它做减速运动,且t=T时,速度恰好为0,之后重复该周期内的运动,直到达到N极板.
又
| L |
| x |
| 0.145 |
| 2.5×10-2 |
故时间t应在2.5T到3T之间,2.5T后,粒子做减速运动,x′=d-5.5×2x=0.02m
粒子的加速度大小也是a,由公式:x′=vt+
| 1 |
| 2 |
得:x′=a
| T |
| 2 |
| 1 |
| 2 |
代入数据,解得:t′=5.53×10-4s
总时间为:t总=2.5T+t′=5.553×10-3s
(2)由题意得,运动的时间是周期的整数倍,没打到极板上.粒子在电场中做加速-减速运动,没打到极板上,说明沿着电场线方向的位移不超过
| d |
| 2 |
| t总 |
| 2 |
解得:v0=100m/s
答:(1)粒子从M板运动到N板所经历的时间是5.553×10-3;
(2)粒子沿水平方向离开电场,求初速度v0的大小为100m/s.
点评:该题考查带电粒子在电场中 的运动,由于电场具有周期性,因此粒子的运动也有周期性,在解题的过程中要抓住这一特征.属于难题.

练习册系列答案
相关题目

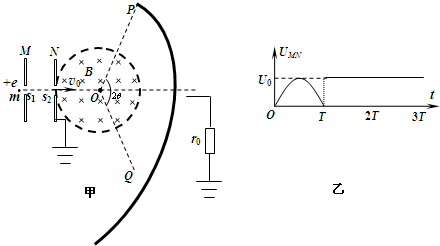
 (2012?嘉兴二模)如图甲所示,M、N为竖直放置的两块平行金属板,圆形虚线为与N相连且接地的圆形金属网罩.PQ为与圆形网罩同心的金属收集屏,通过阻值为r0的电阻与大地相连.小孔s1、s2、圆心O与PQ中点位于同一水平线上.圆心角2θ=120°、半径为R的网罩内有大小为B,方向垂直纸面向里的匀强磁场.M、N间相距
(2012?嘉兴二模)如图甲所示,M、N为竖直放置的两块平行金属板,圆形虚线为与N相连且接地的圆形金属网罩.PQ为与圆形网罩同心的金属收集屏,通过阻值为r0的电阻与大地相连.小孔s1、s2、圆心O与PQ中点位于同一水平线上.圆心角2θ=120°、半径为R的网罩内有大小为B,方向垂直纸面向里的匀强磁场.M、N间相距