题目内容
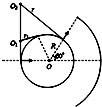
 (2012?嘉兴二模)如图甲所示,M、N为竖直放置的两块平行金属板,圆形虚线为与N相连且接地的圆形金属网罩.PQ为与圆形网罩同心的金属收集屏,通过阻值为r0的电阻与大地相连.小孔s1、s2、圆心O与PQ中点位于同一水平线上.圆心角2θ=120°、半径为R的网罩内有大小为B,方向垂直纸面向里的匀强磁场.M、N间相距
(2012?嘉兴二模)如图甲所示,M、N为竖直放置的两块平行金属板,圆形虚线为与N相连且接地的圆形金属网罩.PQ为与圆形网罩同心的金属收集屏,通过阻值为r0的电阻与大地相连.小孔s1、s2、圆心O与PQ中点位于同一水平线上.圆心角2θ=120°、半径为R的网罩内有大小为B,方向垂直纸面向里的匀强磁场.M、N间相距| R |
| 2 |
| π |
| T |
| 3eB2R2 |
| m |
(1)质子在哪些时间段内自s1处进入板间,穿出磁场后均能打到收集屏PQ上?
(2)质子从进入s1到穿出金属网罩经历的时间记为t′,写出t′与UMN之间的函数关系(tanx=a 可表示为x=arctana)
(3)若毎秒钟进入s1的质子数为n,则收集屏PQ电势稳定后的发热功率为多少?
分析:(1)质子在MN板间运动,由动能定理求出加速获得的速度.质子在磁场中做匀速圆周运动,由洛伦兹力提供向心力,根据牛顿第二定律求出质子轨迹半径与电压UMN的关系式.由题意,2θ=120°,若质子能打在收集屏上,轨道半径r与半径R应满足的关系:r≥
R,联立可得到板间电压UMN的范围,即可求出时间范围.
(2)质子在电场中做匀加速运动,由运动学公式求出时间;根据磁场中轨迹的圆心角α,由t=
T求磁场中运动的时间.即可得到总时间.
(3)稳定时,收集屏上电荷不再增加,即在t>T 时刻以后,UMN=U0,收集屏与地面电势差恒为U,单位时间到达收集板的质子数n,单位时间内,质子的总能量为P总,单位时间内屏上发热功率为P屏=P总-P热,消耗在电阻上的功率为P热=I2r0,所以收集板发热功率 P板=P总-P热,联立求解.
| 3 |
(2)质子在电场中做匀加速运动,由运动学公式求出时间;根据磁场中轨迹的圆心角α,由t=
| α |
| 2π |
(3)稳定时,收集屏上电荷不再增加,即在t>T 时刻以后,UMN=U0,收集屏与地面电势差恒为U,单位时间到达收集板的质子数n,单位时间内,质子的总能量为P总,单位时间内屏上发热功率为P屏=P总-P热,消耗在电阻上的功率为P热=I2r0,所以收集板发热功率 P板=P总-P热,联立求解.
解答:解:(1)质子在MN板间运动,根据动能定理,有eUMN=
m
得 v0=
质子在磁场中运动,根据牛顿第二定律,有
evB=m
联立 r=
=
若质子能打在收集屏上,轨道半径r与半径R应满足的关系:r≥
R
解得板间电压 UMN≥
结合图象可知:质子在
≤t≤
T和t≥T之间任一时刻从s1处进入电场,均能打到收集屏上
(2)M、N间的电压越小,质子穿出电场进入磁场时的速度越小,质子在极板间经历的时间越长,同时在磁场中运动轨迹的半径越小,在磁场中运动的时间也会越长,设在磁场中质子运动所对应的圆半径为r,运动圆弧所对应的圆心角为θ,射出电场的速度为v0,质子穿出金属网罩时,对应总时间为t,则
在板间电场中运动时间t1=
=
=R
tan
=
=
=
在磁场中运动时间t2=
=
所以,运动总时间t=t1+t2=R
+
,θ=2arctan
在磁场中运动时间t2=
=
=
arctan
所以,运动总时间t=t1+t2=R
+
arctan
(3)稳定时,收集屏上电荷不再增加,即在t>T 时刻以后,此时,UMN=U0,收集屏与地面电势差恒为U,U=Ir0
单位时间到达收集板的质子数n
单位时间内,质子的总能量为P总=
nm
=neU0=IU0
单位时间内屏上发热功率为P屏=P总-P热
消耗在电阻上的功率为P热=I2r0
所以收集板发热功率 P板=P总-P热=IU0-I2r0=neU0-n2e2r0
答:(1)质子在
≤t≤
T和t≥T之间任一时刻从s1处进入电场,均能打到收集屏上;
(2)出t′与UMN之间的函数关系是t=R
+
arctan
;
(3)收集屏PQ电势稳定后的发热功率为neU0-n2e2r0.
| 1 |
| 2 |
| v | 2 0 |
得 v0=
|
质子在磁场中运动,根据牛顿第二定律,有
evB=m
| ||
| r |

联立 r=
| mv0 |
| eB |
| 1 |
| B |
|
若质子能打在收集屏上,轨道半径r与半径R应满足的关系:r≥
| 3 |
解得板间电压 UMN≥
| 3eB2R2 |
| 2m |
结合图象可知:质子在
| T |
| 6 |
| 5 |
| 6 |
(2)M、N间的电压越小,质子穿出电场进入磁场时的速度越小,质子在极板间经历的时间越长,同时在磁场中运动轨迹的半径越小,在磁场中运动的时间也会越长,设在磁场中质子运动所对应的圆半径为r,运动圆弧所对应的圆心角为θ,射出电场的速度为v0,质子穿出金属网罩时,对应总时间为t,则
在板间电场中运动时间t1=
| ||
|
| R |
| v0 |
|
tan
| θ |
| 2 |
| R |
| r |
| RBe |
| mv0 |
| RBe | ||
|
在磁场中运动时间t2=
| Rθ |
| v0 |
| θm |
| Be |
所以,运动总时间t=t1+t2=R
|
| θm |
| Be |
| RBe |
| mv0 |
在磁场中运动时间t2=
| Rθ |
| v0 |
| θm |
| Be |
| 2m |
| Be |
| RBe | ||
|
所以,运动总时间t=t1+t2=R
|
| 2m |
| Be |
| RBe | ||
|
(3)稳定时,收集屏上电荷不再增加,即在t>T 时刻以后,此时,UMN=U0,收集屏与地面电势差恒为U,U=Ir0
单位时间到达收集板的质子数n
单位时间内,质子的总能量为P总=
| 1 |
| 2 |
| v | 2 0 |
单位时间内屏上发热功率为P屏=P总-P热
消耗在电阻上的功率为P热=I2r0
所以收集板发热功率 P板=P总-P热=IU0-I2r0=neU0-n2e2r0
答:(1)质子在
| T |
| 6 |
| 5 |
| 6 |
(2)出t′与UMN之间的函数关系是t=R
|
| 2m |
| Be |
| RBe | ||
|
(3)收集屏PQ电势稳定后的发热功率为neU0-n2e2r0.
点评:本题要注意质子在电场中加速后进入磁场中偏转;加速电场中由动能定理求出速度,而在磁场中的运动要由几何关系确定圆心和半径,再根据牛顿第二定律及向心力公式列式求解.本题中的难点在于找出时间范围及时间的最大值.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
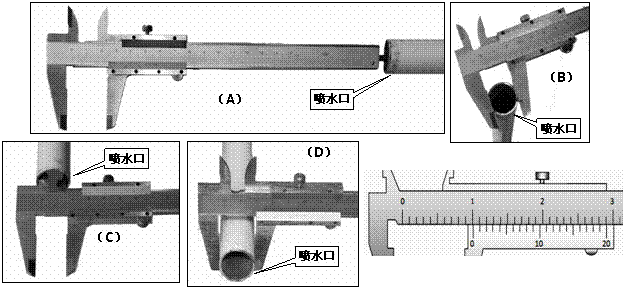
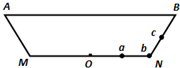 (2012?嘉兴二模)如图为某一水池的竖直截面,AB为水面,MN为水平池底,图中a、b、c为三个相同的发光点,位于N的发光点b发出的光恰能经水面全反射到达池底中央O点处,则( )
(2012?嘉兴二模)如图为某一水池的竖直截面,AB为水面,MN为水平池底,图中a、b、c为三个相同的发光点,位于N的发光点b发出的光恰能经水面全反射到达池底中央O点处,则( )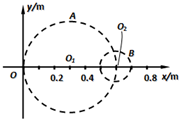 (2012?嘉兴二模)如图所示,在一平静水面上建立xOy坐标系,甲 乙两波源分别在O1 和O2位置先后以5Hz的频率上下振动,图中A、B为某一时刻两波刚到达的位置.波传播过程中能量损耗不计.图示时刻x=0.4m处的质点沿振动方向的位移为零,速度向下.已知水波的波速为0.5m/s,振幅为2cm,两波源起振方式相同,则下列说法正确的是( )
(2012?嘉兴二模)如图所示,在一平静水面上建立xOy坐标系,甲 乙两波源分别在O1 和O2位置先后以5Hz的频率上下振动,图中A、B为某一时刻两波刚到达的位置.波传播过程中能量损耗不计.图示时刻x=0.4m处的质点沿振动方向的位移为零,速度向下.已知水波的波速为0.5m/s,振幅为2cm,两波源起振方式相同,则下列说法正确的是( )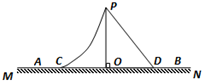 (2012?嘉兴二模)如图所示,曲面PC和斜面PD固定在水平面MN上,C、D处平滑连接,O点位于斜面顶点P的正下方.某人从顶端P由静止开始分别沿曲面和斜面滑下,经过C、D两点后继续运动,最后停在水平面的A、B两处.各处材质相同,忽略空气阻力,则( )
(2012?嘉兴二模)如图所示,曲面PC和斜面PD固定在水平面MN上,C、D处平滑连接,O点位于斜面顶点P的正下方.某人从顶端P由静止开始分别沿曲面和斜面滑下,经过C、D两点后继续运动,最后停在水平面的A、B两处.各处材质相同,忽略空气阻力,则( )