题目内容
如图甲所示,M、N为水平放置的平行板电容器的两个极板,两极板间距d=0.1m,两极板间的电压U=12.5V,O为上极板中心的小孔,以O为坐标原点,在竖直平面内建立直角坐标系,在y轴方向上,0≤y≤2m区间存在方向与x轴平行的匀强电场(PQ为电场区域的上边界),在x轴方向上,电场范围足够大.若规定x轴正方向为电场正方向,电场强度随时间变化情况如图乙所示.现有一个带负电的粒子,在t=0时刻从紧靠M级板中心O'处无初速释放,经过小孔O进入N板上方的交变电场中,粒子的比荷q/m=1×102C/kg,不计粒子重力.求:
(1)粒子进入交变电场时的速度.
(2)粒子在两板之间飞行的时间.
(3)粒子在8×10-3s末的位置坐标.
(4)粒子离开交变电场时的速度大小和方向.

(1)粒子进入交变电场时的速度.
(2)粒子在两板之间飞行的时间.
(3)粒子在8×10-3s末的位置坐标.
(4)粒子离开交变电场时的速度大小和方向.
分析:(1)根据动能定理,电场力做功等于粒子动能的变化求粒子进入交变电场时的速度;
(2)在加速电场中,粒子做匀加速运动,先根据牛顿第二定律求解加速度,然后根据速度时间关系公式求解加速时间;
(3)根据粒子受力情况,确定粒子做类平抛运动,根据运动特征求出粒子的位置坐标;
(4)求出粒子在交变电场中的运动规律,根据交变电场的周期性确定粒子的运动情况.
(2)在加速电场中,粒子做匀加速运动,先根据牛顿第二定律求解加速度,然后根据速度时间关系公式求解加速时间;
(3)根据粒子受力情况,确定粒子做类平抛运动,根据运动特征求出粒子的位置坐标;
(4)求出粒子在交变电场中的运动规律,根据交变电场的周期性确定粒子的运动情况.
解答:解:(1)粒子经过加速电压,根据动能定理:qU=
mv02---①
解得:v0=50m/s
(2)在加速电场中,粒子做匀加速运动:a=
=1.25×104m/s2
故飞行时间为t=
=4×10-3 s
(3)粒子在t=4×10-3 s时进入交变电场,受到水平向右的电场力做类平抛运动:
加速度:a′=
=4×103m/s2
沿+y轴方向粒子匀速运动:y=v0t----②
沿+x轴方向粒子做匀加速运动:x=
a′t2----③
解②③得:x=0.032m,y=0.2m
故粒子在8×10-3 s末的位置坐标为(0.032m,0.2m)
(4)沿+y轴方向粒子始终做匀速运动,0<y<2m区间内:
粒子运动的时间t=
=4×10-2s=5T(运动的总时间是交变电压周期的5倍)
故粒子沿x轴方向速度为0,粒子离开交变电场时速度方向沿+y方向,大小50m/s.
答:(1)进入交变电场时的速度v0=50m/s;
(2)粒子在两板之间飞行的时间为4×10-3 s;
(3)在8×10-3s末的位置坐标(0.032m,0.2m);
(4)离开交变电场时的速度大小为50m/s和方向竖直向上.
| 1 |
| 2 |
解得:v0=50m/s
(2)在加速电场中,粒子做匀加速运动:a=
| Uq |
| dm |
故飞行时间为t=
| v0 |
| a |
(3)粒子在t=4×10-3 s时进入交变电场,受到水平向右的电场力做类平抛运动:
加速度:a′=
| qE |
| m |
沿+y轴方向粒子匀速运动:y=v0t----②
沿+x轴方向粒子做匀加速运动:x=
| 1 |
| 2 |
解②③得:x=0.032m,y=0.2m
故粒子在8×10-3 s末的位置坐标为(0.032m,0.2m)
(4)沿+y轴方向粒子始终做匀速运动,0<y<2m区间内:
粒子运动的时间t=
| y |
| v0 |
故粒子沿x轴方向速度为0,粒子离开交变电场时速度方向沿+y方向,大小50m/s.
答:(1)进入交变电场时的速度v0=50m/s;
(2)粒子在两板之间飞行的时间为4×10-3 s;
(3)在8×10-3s末的位置坐标(0.032m,0.2m);
(4)离开交变电场时的速度大小为50m/s和方向竖直向上.
点评:能根据动能定理求粒子加速后的速度,掌握类平抛运动物体的处理方法是解决本题的关键.

练习册系列答案
相关题目
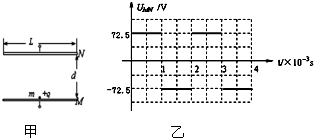 如图甲所示,M、N为水平放置的平行板电容器的两极板,极板长L=0.2m,两板间距d=0.145m,在M、N间加上如图乙所示的电压,一个带电粒子的电量q=+1.0×10-6C、质量m=1.0×10-8kg,粒子重力不计.
如图甲所示,M、N为水平放置的平行板电容器的两极板,极板长L=0.2m,两板间距d=0.145m,在M、N间加上如图乙所示的电压,一个带电粒子的电量q=+1.0×10-6C、质量m=1.0×10-8kg,粒子重力不计.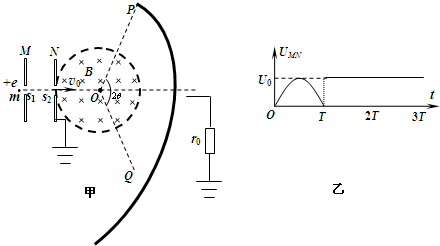
 (2012?嘉兴二模)如图甲所示,M、N为竖直放置的两块平行金属板,圆形虚线为与N相连且接地的圆形金属网罩.PQ为与圆形网罩同心的金属收集屏,通过阻值为r0的电阻与大地相连.小孔s1、s2、圆心O与PQ中点位于同一水平线上.圆心角2θ=120°、半径为R的网罩内有大小为B,方向垂直纸面向里的匀强磁场.M、N间相距
(2012?嘉兴二模)如图甲所示,M、N为竖直放置的两块平行金属板,圆形虚线为与N相连且接地的圆形金属网罩.PQ为与圆形网罩同心的金属收集屏,通过阻值为r0的电阻与大地相连.小孔s1、s2、圆心O与PQ中点位于同一水平线上.圆心角2θ=120°、半径为R的网罩内有大小为B,方向垂直纸面向里的匀强磁场.M、N间相距