题目内容
15. 测量小物块Q与平板P之间的动摩擦因数的实验装置如图所示.AB是半径足够大的较光滑的四分之一圆弧轨道,与水平固定放置的P板的上表面BC在B点相切,C点在水平地面的垂直投影为C′.重力加速度大小为g.实验步骤如下:
测量小物块Q与平板P之间的动摩擦因数的实验装置如图所示.AB是半径足够大的较光滑的四分之一圆弧轨道,与水平固定放置的P板的上表面BC在B点相切,C点在水平地面的垂直投影为C′.重力加速度大小为g.实验步骤如下:①用天平称出物块Q的质量m;
②测量出轨道AB的半径R、BC的长度L和CC′的长度h;
③将物块Q在A点从静止释放,在物块Q落地处标记其落点D;
④重复步骤③,共做10次;
⑤将10个落地点用一个尽量小的圆围住,用米尺测量圆心到C′的距离S.
解答下列问题:
(1)用实验中的测量量表示物块Q与平板P之间的动摩擦因数μ=$\frac{R}{L}-\frac{s^2}{4hL}$(即用字母:R、S、h、L表示);
(2)实验步骤④⑤的目的是减小实验的偶然误差,
(3)若实验测得的μ值比实际值偏大,其原因除了实验中测量量的误差之外,其它的可能是圆弧轨道与滑块间有摩擦.(写出一个可能的原因即可)
分析 (1)物块由A到B点过程,由动能定理可以求出物块到达B时的动能;
物块离开C点后做平抛运动,由平抛运动的知识可以求出物块在C点的速度,然后求出在C点的动能;
由B到C,由动能定理可以求出克服摩擦力所做的功;
由功的计算公式可以求出动摩擦因数.
(2)多次实验的目的是减小实验误差,误差偏大的原因是存在摩擦阻力.
解答 解:(1)①从A到B,由动能定理得:mgR=EKB-0,则物块到达B时的动能:EKB=mgR;
②离开C后,物块做平抛运动,
水平方向:s=vCt,
竖直方向:h=$\frac{1}{2}$gt2,
物块在C点的动能:EKC=$\frac{1}{2}$mvC2,
解得:EKC=$\frac{mg{s}^{2}}{4h}$;
③由B到C过程中,由动能定理得:
-Wf=$\frac{1}{2}$mvC2-$\frac{1}{2}$mvB2,
克服摩擦力做的功:Wf=mgR-$\frac{mg{s}^{2}}{4h}$;
④B到C过程中,克服摩擦力做的功:
Wf=μmgL=mgR-$\frac{mg{s}^{2}}{4h}$,
则:μ=$\frac{R}{L}$-$\frac{{s}^{2}}{4hL}$;
(2)实验步骤④⑤的目的,是通过多次实验减小实验结果的误差;
(3)实验测得的μ值比实际值偏大,其原因除了实验中测量量的误差之外,其他的可能是圆弧轨道存在摩擦,接缝B处不平滑等.
故答案为:(1)$\frac{R}{L}-\frac{s^2}{4hL}$;(2)减小实验的偶然误差;(3)圆弧轨道与滑块间有摩擦.
点评 熟练应用动能定理、平抛运动规律、功的计算公式即可正确解题,学会根据实验数据来实验结果分析,注意实验误差不会没有,只能降低.

练习册系列答案
相关题目
3.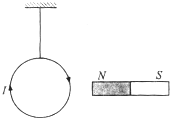 19世纪安培通过比较环形电流的磁场与磁体磁场的相似性,提出了分子电流理论,说明了磁体的磁场和电流的磁场具有相同的起源,即磁现象的电本质.请你通过这种相似性分析说明当把如图所示的载流导体环放置在磁体附近,导体环及悬线的偏转情况是( )
19世纪安培通过比较环形电流的磁场与磁体磁场的相似性,提出了分子电流理论,说明了磁体的磁场和电流的磁场具有相同的起源,即磁现象的电本质.请你通过这种相似性分析说明当把如图所示的载流导体环放置在磁体附近,导体环及悬线的偏转情况是( )
 19世纪安培通过比较环形电流的磁场与磁体磁场的相似性,提出了分子电流理论,说明了磁体的磁场和电流的磁场具有相同的起源,即磁现象的电本质.请你通过这种相似性分析说明当把如图所示的载流导体环放置在磁体附近,导体环及悬线的偏转情况是( )
19世纪安培通过比较环形电流的磁场与磁体磁场的相似性,提出了分子电流理论,说明了磁体的磁场和电流的磁场具有相同的起源,即磁现象的电本质.请你通过这种相似性分析说明当把如图所示的载流导体环放置在磁体附近,导体环及悬线的偏转情况是( )| A. | 从上往下看,导体环顺时针旋转,同时悬线向左偏转 | |
| B. | 从上往下看,导体环逆时针旋转,同时悬线向右偏转 | |
| C. | 导体环不旋转,悬线向右偏转 | |
| D. | 导体环不旋转,悬线向左偏转 |
10.当今社会小汽车已进人家庭成为主要的代步交通工具.考驾照成为热门,科目二考试中的一项内容就是半坡起步.设坡路的倾角为θ,一位考员从半坡由静止以恒定功率P启动,沿坡路向上行驶,车和人的总质量为m,车所受阻力为支持力的k倍,坡路足够长.重力加速度为g.下列说法正确的是( )
| A. | 汽车先做匀加速运动后做匀速运动 | |
| B. | 汽车能达到的最大速度为$\frac{P}{mgsinθ+kmgcosθ}$ | |
| C. | 汽车匀速运动时的牵引力大小等于kmg cosθ | |
| D. | 克服汽车所受阻力做的功等于汽车机械能的增加量 |
20.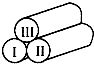 如图所示,编号为Ⅰ、Ⅱ、Ⅲ的三根圆木粗细相同、质量均为m.Ⅰ、Ⅱ并排横放在水平地面上,Ⅲ叠放在Ⅰ、Ⅱ上面,三根圆木均处于静止状态.已知重力加速度g,以下判断正确的是( )
如图所示,编号为Ⅰ、Ⅱ、Ⅲ的三根圆木粗细相同、质量均为m.Ⅰ、Ⅱ并排横放在水平地面上,Ⅲ叠放在Ⅰ、Ⅱ上面,三根圆木均处于静止状态.已知重力加速度g,以下判断正确的是( )
 如图所示,编号为Ⅰ、Ⅱ、Ⅲ的三根圆木粗细相同、质量均为m.Ⅰ、Ⅱ并排横放在水平地面上,Ⅲ叠放在Ⅰ、Ⅱ上面,三根圆木均处于静止状态.已知重力加速度g,以下判断正确的是( )
如图所示,编号为Ⅰ、Ⅱ、Ⅲ的三根圆木粗细相同、质量均为m.Ⅰ、Ⅱ并排横放在水平地面上,Ⅲ叠放在Ⅰ、Ⅱ上面,三根圆木均处于静止状态.已知重力加速度g,以下判断正确的是( )| A. | Ⅰ对Ⅲ的支持力大小为$\frac{1}{2}$mg | B. | Ⅰ对Ⅲ的支持力大小为$\frac{\sqrt{3}}{3}$mg | ||
| C. | 地面对I的摩擦力大小为$\frac{\sqrt{3}}{6}$mg | D. | 地面对I的摩擦力大小为0 |
7.下列说法正确的是( )
| A. | 硬币或钢针能浮于水面上,是由于液体表面张力的作用 | |
| B. | 晶体有固定的熔点,具有规则的几何外形,物理性质具有各向异性 | |
| C. | 影响蒸发快慢以及影响人们对干爽与潮湿感受的因素是空气中水蒸气的压强与同一温度下水的饱和汽压的差距 | |
| D. | 随着科技的发展,将来可以利用高科技手段,将散失在环境中的内能重新收集起来加以利用而不引起其他变化 |
4.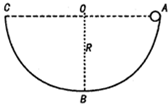 如图所示,竖直平面内有一光滑绝缘半圆轨道,处于方向水平且与轨道平面平行的匀强电场中,轨道两端点A、C高度相同,与圆心O在同一水平线上,轨道的半径为R0,一个质量为m的带正电的小球从槽右端的A处无初速地沿轨道下滑,滑到最低点B时对槽底的压力为2mg,则在小球的滑动过程中,有( )
如图所示,竖直平面内有一光滑绝缘半圆轨道,处于方向水平且与轨道平面平行的匀强电场中,轨道两端点A、C高度相同,与圆心O在同一水平线上,轨道的半径为R0,一个质量为m的带正电的小球从槽右端的A处无初速地沿轨道下滑,滑到最低点B时对槽底的压力为2mg,则在小球的滑动过程中,有( )
 如图所示,竖直平面内有一光滑绝缘半圆轨道,处于方向水平且与轨道平面平行的匀强电场中,轨道两端点A、C高度相同,与圆心O在同一水平线上,轨道的半径为R0,一个质量为m的带正电的小球从槽右端的A处无初速地沿轨道下滑,滑到最低点B时对槽底的压力为2mg,则在小球的滑动过程中,有( )
如图所示,竖直平面内有一光滑绝缘半圆轨道,处于方向水平且与轨道平面平行的匀强电场中,轨道两端点A、C高度相同,与圆心O在同一水平线上,轨道的半径为R0,一个质量为m的带正电的小球从槽右端的A处无初速地沿轨道下滑,滑到最低点B时对槽底的压力为2mg,则在小球的滑动过程中,有( )| A. | 小球到达B点时的速度大小为$\sqrt{2gR}$ | |
| B. | 小球到达B点时的速度大小为$\sqrt{gR}$ | |
| C. | 小球在滑动过程中的最大速度为$\sqrt{(\sqrt{5}-1)gR}$ | |
| D. | 小球在滑动过程中的最大速度为$\sqrt{2gR}$ |
5.图中实线和虚线分别是x轴上传播的一列简谐横波在t=0和t=0.03s时刻的波形图,已知x=1.2m处的质点在t=0.03s时刻向y轴正方向运动,则( )
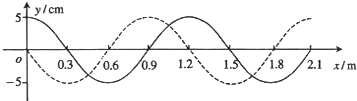

| A. | 各质点在0.03s内随波迁移0.9m | |
| B. | 该波的频率可能是125HZ | |
| C. | 该波的波速可能是10m/s | |
| D. | t=0时x=1.4m处质点的加速度方向沿y轴正方向 |
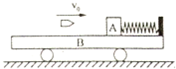 如图所示,质量M=9kg小车B静止在光滑水平面上,小车右端固定一轻质弹簧,质量m=0.9kg的木块A(可视为质点)紧靠弹簧放置并处于静止状态,A与弹簧不栓接,弹簧处于原长状态.木块A右侧车上表面光滑,木块A左侧车表面粗糙,动摩擦因数μ=0.75.一颗质量m0=0.1kg的子弹以v0=100m/s的速度水平向右飞来,瞬间击中木块并留在其中.如果最后木块A刚好不从小车左端掉下来,
如图所示,质量M=9kg小车B静止在光滑水平面上,小车右端固定一轻质弹簧,质量m=0.9kg的木块A(可视为质点)紧靠弹簧放置并处于静止状态,A与弹簧不栓接,弹簧处于原长状态.木块A右侧车上表面光滑,木块A左侧车表面粗糙,动摩擦因数μ=0.75.一颗质量m0=0.1kg的子弹以v0=100m/s的速度水平向右飞来,瞬间击中木块并留在其中.如果最后木块A刚好不从小车左端掉下来,