题目内容
6．
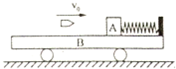如图所示，质量M=9kg小车B静止在光滑水平面上，小车右端固定一轻质弹簧，质量m=0.9kg的木块A（可视为质点）紧靠弹簧放置并处于静止状态，A与弹簧不栓接，弹簧处于原长状态．木块A右侧车上表面光滑，木块A左侧车表面粗糙，动摩擦因数μ=0.75．一颗质量m0=0.1kg的子弹以v0=100m/s的速度水平向右飞来，瞬间击中木块并留在其中．如果最后木块A刚好不从小车左端掉下来，求：小车最后的速度及最初木块A到小车左端的距离．
分析 平板车与木块组成的系统动量守恒，由动量守恒定律可以求出速度．由动能的计算公式可以求出动能．由能量守恒定律可以求出木块A到小车左端的距离．
解答 解：当平板车与木块速度相同时，弹簧被压缩到最短，设此时速度为V1，以木块、木板、弹簧为系统，系统动量守恒，以木块的初速度方向为正方向，由动量守恒定律得：
m0v0=（M+m+m0）v1
v1=1m/s
子弹进入木块的过程中动量守恒，得：m0v0=（m+m0）v2
v2=10m/s
滑块在小车是滑动的过程中：$\frac{1}{2}$（m+m0）v22-$\frac{1}{2}$（M+m+m0） v12=μmgL
联立解得：L=6m
答：小车最后的速度是1m/s；木块A到小车左端的距离是6m．
点评 本题考查了求速度、动能、弹性势能，分析清楚物体运动过程、应用动量守恒定律、能量守恒定律即可正确解题．
练习册系列答案
相关题目
16．
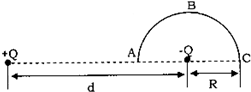对于真空中电荷量为q的静止点电荷而言，当选取离点电荷无穷远的电势为零时，离点电荷距离为r的位置的电势为φ=$\frac{kq}{r}$（k为静电力常量），如图所示，两电荷量大小均为Q的异种点电荷相距为d，现将一质子（电荷量为+e）从两电荷连线上的A点沿以负电荷为圆心、半径为R的半圆形轨迹ABC移到C点，在质子从A到C的过程中，系统电势能的变化情况为（ ）
对于真空中电荷量为q的静止点电荷而言，当选取离点电荷无穷远的电势为零时，离点电荷距离为r的位置的电势为φ=$\frac{kq}{r}$（k为静电力常量），如图所示，两电荷量大小均为Q的异种点电荷相距为d，现将一质子（电荷量为+e）从两电荷连线上的A点沿以负电荷为圆心、半径为R的半圆形轨迹ABC移到C点，在质子从A到C的过程中，系统电势能的变化情况为（ ）| A． | 减少$\frac{2k{Q}_{e}}{{d}^{2}-{R}^{2}}$ | B． | 增加$\frac{2k{Q}_{e}R}{{d}^{2}+{R}^{2}}$ | ||
| C． | 减少$\frac{2k{Q}_{e}R}{{d}^{2}-{R}^{2}}$ | D． | 增加$\frac{2k{Q}_{e}}{{d}^{2}+{R}^{2}}$ |
14．探月工程三期飞行试验器于2014年10月24日2时在中国西昌卫星发射中心发射升空，最终进入距月球表面高为h的圆形工作轨道，设月球半径为R，月球表面的重力速度为g，万有引力常量为G，则下列说法正确的是（ ）
| A． | 飞行试验器在工作轨道上的加速度为（$\frac{R}{R+h}$）2g | |
| B． | 飞行试验器绕月球运行的周期为2π$\sqrt{\frac{R}{g}}$ | |
| C． | 飞行试验器在工作轨道上的绕行速度为$\sqrt{g（R+h）}$ | |
| D． | 月球的平均密度为$\frac{3g}{4πGR}$ |
1．下列说法中正确的是（ ）
| A． | 核反应方程${\;}_{90}^{234}$Th→${\;}_{91}^{234}$Pa+X中的X表示质子 | |
| B． | 卢瑟福通过对a粒子散射实验结果的分析，提出了原子的核式结构模型 | |
| C． | 放射性元素的半衰期与外界的温度有关 | |
| D． | α，β和γ三种射线中，γ射线的穿透能力最强 |
测量小物块Q与平板P之间的动摩擦因数的实验装置如图所示．AB是半径足够大的较光滑的四分之一圆弧轨道，与水平固定放置的P板的上表面BC在B点相切，C点在水平地面的垂直投影为C′．重力加速度大小为g．实验步骤如下：
16．
如图所示为一个简易测温装置，玻璃瓶装半瓶带颜色的水，用软木塞塞紧．软木塞上插进一根一端密闭的细玻璃管．若加热玻璃瓶内的水，则（ ）
如图所示为一个简易测温装置，玻璃瓶装半瓶带颜色的水，用软木塞塞紧．软木塞上插进一根一端密闭的细玻璃管．若加热玻璃瓶内的水，则（ ）| A． | 细玻璃管内气体密度增大 | B． | 外界对细玻璃管内气体做正功 | ||
| C． | 细玻璃管内气体压强不变 | D． | 细玻璃管内气体的平均动能增加 |