题目内容
【题目】如图，一小车上有一个固定的水平横杆，左边有一轻杆与竖直方向成θ角与横杆固定，下端连接一质量为m的小球P，横杆右边用一根细线吊一相同的小球Q．当小车沿水平面做加速运动时，细线保持与竖直方向的夹角为α．已知θ＜α，不计空气阻力，重力加速度为g，则下列说法正确的是
A. 小车一定向右做匀加速运动
B. 轻杆对小球P的弹力沿轻杆方向
C. 小球P受到的合力不一定沿水平方向
D. 小球Q受到的合力大小为mgtanα
【答案】D
【解析】对细线吊的小球研究，根据牛顿第二定律，得mgtanα=ma，得到a=gtanα，故加速度向右，小车向右加速，或向左减速，故A错误；由牛顿第二定律，得：mgtanβ=ma′，因为a=a′，得到β=α＞θ，则轻杆对小球的弹力方向与细线平行，故B错误；小球P和Q的加速度相同，水平向右，则两球的合力均水平向右，大小F合=ma=mgtanα，故C错误，D正确．故选D．
练习册系列答案
相关题目
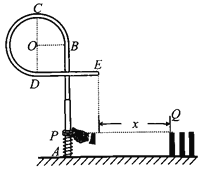
【题目】某同学在做探究弹力和弹簧伸长量的关系的实验中，设计了如图所示的实验装置．他先测出不挂钩码时弹簧的自然长度，再将钩码逐个挂在弹簧的下端，每次都测出相应的弹簧总长度，将数据填在下面的表中．（弹簧始终在弹性限度内）
测量次序 |
|
|
|
|
|
|
弹簧弹力大小 |
|
|
|
|
|
|
弹簧总长 |
|
|
|
|
|
|
（
）下图的坐标纸上已描出了前四次测量的弹簧所受弹力大小
跟弹簧总长
之间的函数关系点，请把第
、
次测量的数据对应的点描出来，并作
图线．
（
）图线跟
坐标轴交点的物理意义是______________________________．
（
）该弹簧的劲度系数
__________
．（保留两位有效数字）