Question

【题目】某同学在设计连锁机关游戏中，设计了如图所示的起始触发装置，AB段是长度连续可调的竖直伸缩杆，BCD段是半径为R的四分之三圆弧弯杆，DE段是长度为2R的水平杆，与AB杆稍稍错开。竖直杆外套有下端固定且劲度系数较大的轻质弹簧，在弹簧上端放置质量为m的套环。每次将弹簧的长度压缩至P点后锁定，设PB的高度差为h，解除锁定后弹簧可将套环弹出。在触发器的右侧有多米诺骨牌，多米诺骨牌的最高点Q和P等高，且与E的水平距离x=8R，已知弹簧锁定时的弹性势能EP=9mgR，套环与水平杆的动摩擦因数为0.5，与其他部分的摩擦不计，重力加速度为g。求：

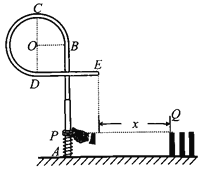
（1）当h=3R时，套环达到杆最高点C处的速度大小。

（2）在上问中当套环运动到最高点C时对杆的作用力大小和方向

（3）若h可在R~6R连续可调，要使该套环恰好击中Q点，则h需调节为多长？

Answer 1

【答案】（1） （2）9mg（3）5R

【解析】（1）当h=3R时，套环从P点运动到C点，根据机械能守恒定律有：E＝mg(h+R)+mv2，E=9mgR
解得：v＝
（2）在最高点C时，对套环，根据牛顿第二定律有：mg+FC=m

解得：FC=9mg，方向竖直向下；
（3）套环恰能击中Q点，平抛运动过程：
hR＝gt2
x=vEt
从P到E，根据能量守恒定律有：E＝mg(hR)+μmg2R+mvE2
联立解得：h=5R