题目内容
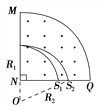
【题目】如图所示，离子源A产生的初速度为零、带电荷量为e、质量不同的正离子被电压为U1的加速电场加速后进入一电容器中，电容器两极板之间的距离为d，电容器中存在磁感应强度大小为B的匀强磁场和匀强电场。正离子能沿直线穿过电容器，垂直于边界MN进入磁感应强度大小也为B的扇形匀强磁场中，∠MNQ＝90°。(不计离子的重力)求：
（1）求质量为m的离子进入电容器时，电容器两极板间的电压U2；
（2）求质量为m的离子在磁场中做圆周运动的半径；
（3）若质量为4m的离子垂直打在NQ的中点S1处，质量为16m的离子打在S2处。求S1和S2之间的距离以及能打在NQ上正离子的质量范围。
【答案】(1)Bd
(2) 
(3) 
m≤mx≤25m
【解析】(1)设离子经加速电场后获得的速度为v1，应用动能定理有U1e＝
mv12
离子进入电容器后沿直线运动，有
＝Bev1 得U2＝Bd
(2)离子在匀强磁场中做匀速圆周运动，由洛伦兹力提供向心力，Bev1＝m
得离子的运动半径R＝
(3)根据(2)中R＝
，质量为4m的离子在磁场中运动打在S1处，运动半径为
R1＝
质量为16m的离子在磁场中运动打在S2处，运动半径为R2＝
又ON＝R2－R1
由几何关系可知S1和S2之间的距离ΔS＝
－R1
联立解得ΔS＝2(
－1) 
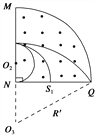
由R′2＝(2R1)2＋(R′－R1)2
解得R′＝
R1
再根据
R1≤Rx≤
R1 解得m≤mx≤25m
【题目】利用电流表和电压表测定一节干电池的电动势和内电阻。要求尽量减小实验误差。
（1）应该选择的实验电路是图中的________(选填“甲”或“乙”)。
（2）某位同学记录的6组数据如下表所示，其中5组数据的对应点已经标在图中的坐标纸上，请标出余下一组数据的对应点，并画出U－I图线________。
序号 | 1 | 2 | 3 | 4 | 5 | 6 |
电压U/V | 1.45 | 1.40 | 1.30 | 1.25 | 1.20 | 1.10 |
电流I/A | 0.060 | 0.120 | 0.240 | 0.260 | 0.360 | 0.480 |
（3）根据（2）中所画图线可得出干电池的电动势E＝________V，内电阻r＝________Ω。
（4）实验中，随着滑动变阻器滑片的移动，电压表的示数U及干电池的输出功率P都会发生变化。下图的各示意图中正确反映P－U关系的是________。
